Question

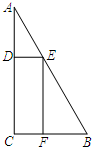（2012•和平区一模）一块三角形废料如图所示，∠A=30°，∠C=90°，AB=12．用这块废料剪出一个矩形CDEF，其中，点D、E、F分别在AC、AB、BC上．要使剪出的矩形CDEF面积最大，点E应选在何处？

Answer 1

分析：首先在Rt△ABC中利用∠A=30°、AB=12，求得BC=6、AC的长，然后根据四边形CDEF是矩形得到EF∥AC从而得到△BEF∽△BAC，设AE=x，则BE=12-x．利用相似三角形成比例表示出EF、DE，然后表示出有关x的二次函数，然后求二次函数的最值即可．

解答：解：在Rt△ABC中，∠A=30°，AB=12，
∴BC=6，AC=AB•cos30°=12×

3

2

=6

3

．
∵四边形CDEF是矩形，
∴EF∥AC．
∴△BEF∽△BAC．
∴

EF

AC

=

BE

BA

．
设AE=x，则BE=12-x．
EF=

6 3 (12-x)

12

=

3

2

(12-x)．
在Rt△ADE中，DE=

1

2

AE=

1

2

x．                   
矩形CDEF的面积S=DE•EF=

1

2

x•

3

2

(12-x)=-

3

4

x2+3

3

x（0＜x＜6）．                
当x=-

b

2a

=-

3 3

2×(- 3 4 )

=6时，S有最大值．
∴点E应选在AB的中点处．

点评：本题考查了相似三角形的应用及二次函数的应用，解题的关键是从几何问题中整理出二次函数模型，并利用二次函数的知识求最值．