题目内容
【题目】综合与实践
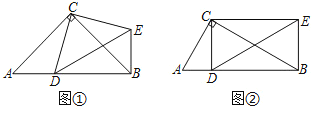
在Rt△ABC中，∠ACB＝90°，点D为斜边AB上的动点（不与点A，B重合）．
（1）操作发现：如图①，当AC＝BC＝8时，把线段CD绕点C逆时针旋转90°得到线段CE，连接DE，BE．
①∠CBE的度数为 ；
②当BE＝ 时，四边形CDBE为正方形；
（2）探究证明：如图②，当BC＝2AC时，把线段CD绕点C逆时针旋转90°后并延长为原来的两倍，记为线段CE，连接DE，BE．
①在点D的运动过程中，请判断∠CBE与∠A的大小关系，并证明；
②当CD⊥AB时，求证：四边形CDBE为矩形．
【答案】（1）①45°；②
；（2）①∠CBE＝∠A，证明详见解析；②详见解析
【解析】
(1)①根据等腰直角三角形的性质得到
，证明
，根据全等三角形的性质证明结论；
②根据勾股求出AB，再根据正方形的性质计算即可；
（2）①证明
，根据相似三角形的性质证明结论；
②根据全等三角形的性质、矩形的判定定理证明．
解：（1）①∵
，
∴，
，
∴∠ACB=∠DCE，
∴
，
即
，
在
和
中，
，
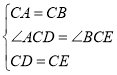∴（SAS），
；
故答案为：45°；
②
,
，
当四边形CDBE是正方形时，CD⊥AB，BE=BD=AD，
；
故答案为：．
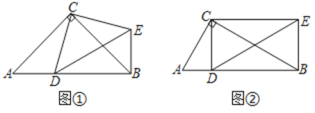
（2）①∠CBE＝∠A．
理由如下：
∵BC＝2AC，CE＝2CD，
∴
，
∵∠ACB＝∠DCE＝90°，
∴∠ACD+∠DCB＝∠DCB+∠BCE，
∴∠ACD＝∠BCE，
∴△ACD∽△BCE，
∴∠CBE＝∠A；
②证明：∵∠CBE＝∠A，∠DBC+∠A＝90°，
∴∠DBE＝∠DBC+∠CBE＝∠DBC+∠A＝90°，
∵
∴∠CDB＝90°，
又∵∠DCE＝90°，
∴四边形CDBE是矩形．
练习册系列答案
阅读快车系列答案
相关题目
