题目内容
【题目】已知AB为⊙O的直径,点C为![]() 的中点,BD为弦,CE⊥BD于点E,
的中点,BD为弦,CE⊥BD于点E,



(1)如图1,求证:CE=DE;
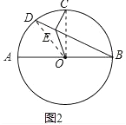
(2)如图2,连接OE,求∠OEB的度数;
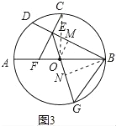
(3)如图3,在(2)条件下,延长CE,交直径AB于点F,延长EO,交⊙O于点G,连接BG,CE=2,EF=3,求△EBG的面积.
【答案】(1)证明见解析;(2)证明见解析;(3)△EBG的面积为6+3![]() .
.
【解析】(1)如图1中,连接CD、OC. 只要证明∠CDE=![]() ∠COB=45°即可.
∠COB=45°即可.
(2)如图2中,连接OD、OC,只要证明△OED≌△OEC,推出∠OED=∠CEO=135°,即可解决问题.
(3)如图3中,过0作OM⊥BD于M,BN⊥EG于N,则∠EMO=90°,连接OC,设EM=x,则BM=DM=2-x,由EF∥OM,得![]() =
=![]() 列出方程即可解决.
列出方程即可解决.
解:(1)证明:如图1中,连接CD、OC.
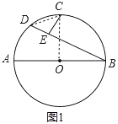
∵点C是AB![]() 中点,∴AC=BC
中点,∴AC=BC![]() ,∴∠AOC=∠BOC,
,∴∠AOC=∠BOC,
∵∠AOC+∠BOC=180°,∴∠AOC=∠BOC=90°,∴∠D=45°,
∵CE⊥BD,∴∠CED=90°,∴∠D=∠DCE=45°,∴CE=DE.
(2)证明:如图2中,连接OD,OC
在△OED和△OEC中,
OC=OD,CE=DE,OE=OE,
∴△OED≌△OEC,
∵∠CED=90°,∴∠OED=∠CEO=135°,∴∠OEB=45°.
(3)解:如图3中,过O作OM⊥BD于M,BN⊥EG于N,则∠EMO=90°,连接OC.
∵CE=2,∴DE=2,设EM=x,则BM=DM=2+x,∴BE=2x+2,∵∠OEB=45°,则BM=DM=2+x,∴OM=x,
∵∠OEB=45°,∴∠CEB=∠EMO,∴EF∥OM.
∴![]()
![]() ,即
,即![]() ,解得x=2或(
,解得x=2或(![]() 舍去),
舍去),
∴OE=2![]()
![]() ,BM=4,OM=2,BN=3
,BM=4,OM=2,BN=3![]()
![]() ,∴OB=2
,∴OB=2![]()
![]() ∴EG=OE+OG=2
∴EG=OE+OG=2![]()
![]() +2
+2![]()
![]() ,
,
∴S△EBG=![]() EGBN=
EGBN=![]() (2
(2![]()
![]() +2
+2![]()
![]() )×3
)×3![]()
![]() =6+3
=6+3![]()
![]() .
.
“点睛”本题考查圆的综合题、全等三角形的判定和性质、平行线的性质、圆的有关知识,解题的关键是灵活应用这些知识解决问题,学会添加常用辅助线,学会用方程的思想思考问题,属于中考压轴题.

 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案