题目内容
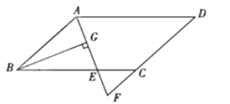
【题目】如图,在Rt△OAB中,OA=4,AB=5,点C在OA上,AC=1,⊙P的圆心P在线段BC上,且⊙P与边AB,AO都相切.若反比例函数![]() (k≠0)的图象经过圆心P,则k=________________。
(k≠0)的图象经过圆心P,则k=________________。

【答案】![]()
【解析】分析:设⊙P与边AB,AO分别相切于点E、D,连接PE、PD、PA,用面积法可求出⊙P的半径,然后通过三角形相似可求出CD,从而得到点P的坐标,就可求出k的值.
详解:设⊙P与边AB,AO分别相切于点E、D,连接PE、PD、PA,如图所示.
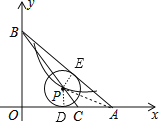
则有PD⊥OA,PE⊥AB.
设⊙P的半径为r,
∵AB=5,AC=1,
∴S△APB= ![]() ABPE=
ABPE=![]() r,S△APC=
r,S△APC=![]() ACPD=
ACPD=![]() r.
r.
∵∠AOB=90°,OA=4,AB=5,
∴OB=3.
∴S△ABC=![]() ACOB=
ACOB=![]() ×1×3=
×1×3=![]() .
.
∵S△ABC=S△APB+S△APC,
∴![]() =
=![]() r+
r+![]() r.
r.
∴r=![]() .
.
∴PD=![]() .
.
∵PD⊥OA,∠AOB=90°,
∴∠PDC=∠BOC=90°.
∴PD∥BO.
∴△PDC∽△BOC.
∴![]() .
.
∴PDOC=CDBO.
∴![]() ×(4-1)=3CD.
×(4-1)=3CD.
∴CD=![]() .
.
∴OD=OC-CD=3-![]() =
=![]() .
.
∴点P的坐标为(![]() ,
,![]() ).
).
∵反比例函数y=![]() (k≠0)的图象经过圆心P,
(k≠0)的图象经过圆心P,
∴k=![]() ×
×![]() =
=![]() .
.
故答案为:![]() .
.

练习册系列答案
相关题目
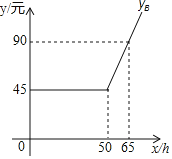
【题目】某通信公司策划了![]() 两种上网的月收费方式:
两种上网的月收费方式:
收费方式 | 月使用费/元 | 包时上网时间/ | 超时费/(元/ |
| 30 | 25 | 0.05 |
|
|
|
|
设每月上网时间为![]() ,方式
,方式![]() 的收费金额分别为
的收费金额分别为![]() (元),
(元),![]() (元),如图是
(元),如图是![]() 与
与![]() 之间函数关系的图象.(友情提示:若累计上网时间不超出包时上网时间,则只收月使用费;若累计上网时间超出包时上网时间,则对超出部分再加收超时费)
之间函数关系的图象.(友情提示:若累计上网时间不超出包时上网时间,则只收月使用费;若累计上网时间超出包时上网时间,则对超出部分再加收超时费)
(1)![]() ,
,![]() ,
,![]() ;
;
(2)求![]() 之间的函数解析式;
之间的函数解析式;
(3)若每月上网时间为31小时,请直接写出选择哪种方式能节省上网费.