Question

【题目】如图，已知等边三角形的边长为，过边上一点作于点，为延长线上一点，取，连接，交于，则的长为______.

Answer 1

【答案】

【解析】

过P作PF∥BC交AC于F，得出等边三角形APF，推出AP=PF=QC，根据等腰三角形性质求出EF=AE，再证△PFM≌△QCM，推出FM=CM，再推出EM=AC即可出结果．

过P作PF∥BC交AC于F，如图所示：

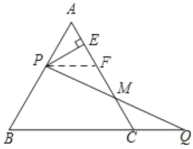
∵PF∥BC，△ABC是等边三角形，

∴∠PFM=∠QCM，∠APF=∠B=60°，∠AFP=∠ACB=60°,∠A=60°，

∴△APF是等边三角形，

∴AP=PF=AF，

∵PE⊥AC，

∴AE=EF，

∵AP=PF，AP=CQ，

∴PF=CQ，

在△PFM和△QCM中，

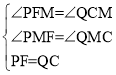
∴△PFM≌△QCM(AAS)，

∴FM=CM，

∵AE=EF，

∴EF+FM=AE+CM，

∴AE+CM=EM=AC，

∵AC=3，

∴EM=，

故答案为：.