题目内容
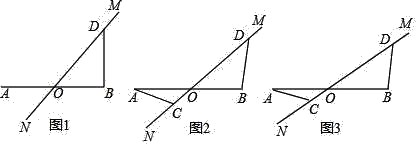
【题目】直线MN与线段AB相交于点O,点C、点D分别为射线ON,OM上两点,且满足∠ACN=∠ODB=45°.
(1)如图1,当点C与点O重合时,且AO=OB,请直接写出AC与BD的数量关系;
(2)将图1中的MN绕点O顺时针旋转α°(0<a<45),如图2所示,若AO=OB,(1)中的AC与BD的数量关系是否仍然成立?若成立,请证明;若不成立,请说明理由;
(3)如图3,若AO=kOB.
①请求出![]() 的值;
的值;
②若k=![]() ,∠AOC=30°,BD=3
,∠AOC=30°,BD=3![]() ,请直接写出OC的长.
,请直接写出OC的长.
【答案】(1)AC=BD;(2)成立;(3)①k;②![]() ;
;
【解析】
(1)先根据∠BOD和∠BDO的度数,判断DB与OB的数量关系以及位置关系,再得出AO与BD的数量关系与位置关系;
(2)先分别过点A,B作AE⊥MN于E,BF⊥MN于F,通过判定△AOE≌△BOF,得到AE=BF,由∠ACN=∠BDN=45°,得∠AEC=∠BFD=90°,求出AC=![]() AE,BD=
AE,BD=![]() BF,得出AC与BD的数量关系;
BF,得出AC与BD的数量关系;
(3)分别过点A,B作AE⊥MN于E,BF⊥MN于F,由△AEO∽△BFO,得![]() ,再求出AC=
,再求出AC=![]() AE,BD=
AE,BD=![]() BF,得出AC与BD的比值.在Rt△ACE中,∠ACE=45°,AE=CE=2,在Rt△AOE中,∠AOE=30°,可得OE=
BF,得出AC与BD的比值.在Rt△ACE中,∠ACE=45°,AE=CE=2,在Rt△AOE中,∠AOE=30°,可得OE=![]() AE=2
AE=2![]() ,可得到OC.
,可得到OC.
解:(1)∵点O和点C重合,
∴AC=OA.∠AON=∠ACN=45°,
∵∠BDO=∠ACN=45°,
∴∠BDO=∠BOD=45°,
∴BD=OB,
∵OA=OB,
∴AC=BD;
(2)成立,理由:如图2,分别过点A,B作AE⊥MN于E,BF⊥MN于F,

∴∠AEC=∠BFO=∠BFD=90°,
在△AOE和△BOF中, ,
,
∴△AOE≌△BOF,
∴AE=BF,
∵∠ACN=∠BDN=45°,
∴∠AEC=∠BFD=90°,
∴AC=![]() AE,BD=
AE,BD=![]() BF,
BF,
∴AC=BD;
(3)①如图3,分别过点A,B作AE⊥MN于E,BF⊥MN于F,
∴∠AEC=∠BFO=∠BFD=90°,
∵∠AOE=∠BOF,
∴△AEO∽△BFO,
∴![]() =k,
=k,
∵∠ACN=∠BDN=45°,
∴∠AEC=∠BFD=90°,
∴AC=![]() AE,BD=
AE,BD=![]() BF,
BF,
∴![]() =k;
=k;
②如图3,由①知,![]() =k,
=k,
∵k=![]() ,BD=3
,BD=3![]() ,
,
∴AC=2![]() ,
,
在Rt△ACE中,∠ACE=45°,
∴AE=CE=2,
在Rt△AOE中,∠AOE=30°,
∴OE=![]() AE=2
AE=2![]() ,
,
∴OC=2(![]() ﹣1).
﹣1).







