ΧβΡΩΡΎ»ί
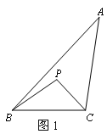
ΓΨΧβΡΩΓΩ»γΆΦΘ§ΓςAEF÷–Θ§ΓœEAF=45ΓψΘ§AGΓΆEF”ΎΒψGΘ§œ÷ΫΪΓςAEG―ΊAE’έΒΰΒΟΒΫΓςAEBΘ§ΫΪΓςAFG―ΊAF’έΒΰΒΟΒΫΓςAFDΘ§―”≥ΛBEΚΆDFœύΫΜ”ΎΒψCΘ°
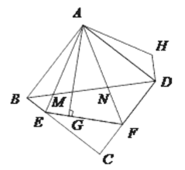
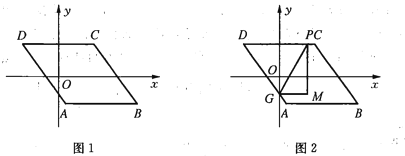
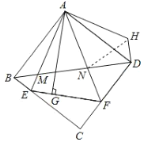
Θ®1Θ© ‘≈–ΕœΥΡ±Ώ–ΈABCDΒΡ–ΈΉ¥Θ§≤ΔΗχ≥ω÷ΛΟςΘΜ
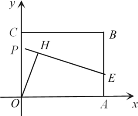
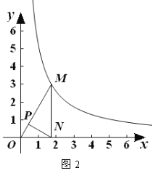
Θ®2Θ©Ν§Ϋ”BDΖ÷±πΫΜAEΓΔAF”ΎΒψMΓΔNΘ§ΫΪΓςABM»ΤΒψAΡφ ±’κ–ΐΉΣΘ§ ΙAB”κAD÷ΊΚœΘ§ΒΟΒΫΓςADHΘ§ ‘≈–ΕœœΏΕΈMNΓΔNDΓΔDH÷°ΦδΒΡ ΐΝΩΙΊœΒΘ§≤ΔΥΒΟςάμ”…Θ°
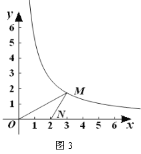
Θ®3Θ©»τEG=2Θ§GF=3Θ§BM=2Θ§«σAGΓΔMNΒΡ≥ΛΘ°
ΓΨ¥πΑΗΓΩΘ®1Θ©ΥΡ±Ώ–Έ![]() «’ΐΖΫ–ΈΘ§ΦϊΫβΈωΘΜΘ®2Θ©
«’ΐΖΫ–ΈΘ§ΦϊΫβΈωΘΜΘ®2Θ©![]() Θ§ΦϊΫβΈωΘΜΘ®3Θ©6Θ§
Θ§ΦϊΫβΈωΘΜΘ®3Θ©6Θ§![]()
ΓΨΫβΈωΓΩ
Θ®1Θ©”…ΆΦ–ΈΖ≠’έ±δΜΜΒΡ–‘÷ Ω…÷ΣΓœABE=ΓœAGE=ΓœBAD=ΓœADC=90ΓψΘ§AB=ADΦ¥Ω…ΒΟ≥ωΫα¬έΘΜ
Θ®2Θ©Ν§Ϋ”NHΘ§”…ΓςABMΓ’ΓςADHΘ§ΒΟAM=AHΘ§BM=DHΘ§ΓœADH=ΓœABD=45ΓψΘ§Ι ΓœNDH=90ΓψΘ§‘Ό÷ΛΓςAMNΓ’ΓςAHNΘ§ΒΟMN=NHΘ§”…Ι¥Ι…Ε®άμΦ¥Ω…ΒΟ≥ωΫα¬έΘΜ
Θ®3Θ©…ηAG=xΘ§‘ρEC=x-2Θ§CF=x-3Θ§‘ΎRtΓςECF÷–Θ§άϊ”ΟΙ¥Ι…Ε®άμΦ¥Ω…ΒΟ≥ωAGΒΡ÷ΒΘ§Ά§άμΩ…ΒΟ≥ωBDΒΡ≥ΛΘ§…ηNH=yΘ§‘ΎRtΓςNHDΘ§άϊ”ΟΙ¥Ι…Ε®άμΦ¥Ω…ΒΟ≥ωMNΒΡ÷ΒΘ°
Θ®1Θ©÷ΛΟςΘΚΓΏΓςAEB”…ΓςAEDΖ≠’έΕχ≥…Θ§
ΓύΓœABE=ΓœAGE=90ΓψΘ§ΓœBAE=ΓœEAGΘ§AB=AGΘ§
ΓΏΓςAFD”…ΓςAFGΖ≠’έΕχ≥…Θ§
ΓύΓœADF=ΓœAGF=90ΓψΘ§ΓœDAF=ΓœFAGΘ§AD=AGΘ§
ΓΏΓœEAG+ΓœFAG=ΓœEAF=45ΓψΘ§
ΓύΓœABE=ΓœAGE=ΓœBAD=ΓœADC=90ΓψΘ§
ΓύΥΡ±Ώ–ΈABCD «ΨΊ–ΈΘ§
ÿAB=ADȧ
ΓύΥΡ±Ώ–ΈABCD «’ΐΖΫ–ΈΘΜ
Θ®2Θ©![]() Θ§
Θ§
άμ”…ΘΚΝ§Ϋ”![]() Θ§
Θ§![]() ”…
”…![]() –ΐΉΣΕχ≥…Θ§
–ΐΉΣΕχ≥…Θ§![]() Θ§
Θ§
![]() Θ§
Θ§![]() Θ§
Θ§
![]() ”…Θ®1Θ©
”…Θ®1Θ©![]() Θ§
Θ§![]() Θ§
Θ§
![]() Θ§
Θ§
![]() Θ§
Θ§
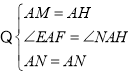 Θ§
Θ§
![]() Θ§
Θ§
![]() Θ§
Θ§
![]() ΘΜ
ΘΜ
Θ®3Θ©…η![]() Θ§‘ρ
Θ§‘ρ![]() Θ§
Θ§![]() Θ§‘Ύ
Θ§‘Ύ![]() ÷–Θ§
÷–Θ§
![]() Θ§
Θ§
Γύ![]() Θ§
Θ§
ΫβΒΟΘ§![]() Θ§
Θ§![]() Θ®…α»ΞΘ©
Θ®…α»ΞΘ©
![]() Θ§
Θ§
![]() Θ§
Θ§![]() Θ§
Θ§
![]() Θ§
Θ§
![]() Θ§
Θ§
![]() Θ§
Θ§
…η![]() Θ§‘Ύ
Θ§‘Ύ![]() ÷–Θ§
÷–Θ§![]() Θ§Φ¥
Θ§Φ¥![]() Θ§
Θ§
ΫβΒΟ![]() Θ§Φ¥
Θ§Φ¥![]() Θ°
Θ°

 ΩΣ–ΡΆήΉ¥‘Σ≤β ‘ΨμœΒΝ–¥πΑΗ
ΩΣ–ΡΆήΉ¥‘Σ≤β ‘ΨμœΒΝ–¥πΑΗ