Question

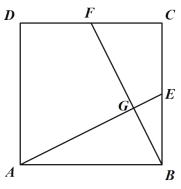
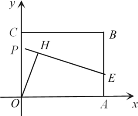
【题目】如图，矩形OABC的边OA、OC分别在x轴、y轴上，点B的坐标为(6，5)，点E在边AB上，且AE=2，已知点P为y轴上一动点，连接EP，过点O作直线EP的垂线段OH，垂足为点H，在点P从点C运动到原点O的过程中，点H的运动路径长为__________．

Answer 1

【答案】

【解析】

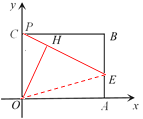
H经过的路径是以OE为直径的弧，连接OE，首先求得△OPE的面积，然后利用三角形面积公式求得OH的长，然后在直角△OEH中，利用三角函数求得∠OEH的度数，然后利用弧长公式即可求解．

∵矩形OABC的边OA、OC分别在x轴、y轴上，点B的坐标为(6，5)，

∴OC=AB=5，BC=AB=6，

连接OE．

当点P与点C重合时，S△OPE= ，

在直角△OEA中，AE=2，OA=6

∴OE=，

PE=，

∵S△OPE=PEOH，即，

∴OH=，

∴在直角△OEH中，sin∠OEH=，

∴∠OEH=45°，

∴点H的运动路径为以OE为直径，从点H到点O的四分之一的圆弧，

故点H的运动路径长是：．

故答案是：．