Ő‚ńŅńŕ»›
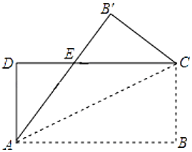
°ĺŐ‚ńŅ°Ņ£®4∑÷£©“Ľ‘™∂Ģīő∑Ĺ≥Ő![]() ĶńłýĶń«ťŅŲ «£® £©
ĶńłýĶń«ťŅŲ «£® £©
A£ģ”–ŃĹłŲ≤ĽŌŗĶ»Ķń Ķ żłý B£ģ”–ŃĹłŲŌŗĶ»Ķń Ķ żłý
C£ģ√Ľ”– Ķ żłý D£ģőř∑®»∑∂®
°ĺīūįł°ŅA£ģ
°ĺĹ‚őŲ°Ņ
‘Ő‚°Ŗ°ų=![]() £¨°ŗ∑Ĺ≥Ő”–ŃĹłŲ≤ĽŌŗĶ»Ķń Ķ żłý£ģĻ —°A£ģ
£¨°ŗ∑Ĺ≥Ő”–ŃĹłŲ≤ĽŌŗĶ»Ķń Ķ żłý£ģĻ —°A£ģ
ŅľĶ„£ļłýĶńŇ–Īū Ĺ£ģ
°ĺŐ‚–Õ°ŅĶ•—°Ő‚
°ĺĹŠ Ý°Ņ
9
°ĺŐ‚ńŅ°Ņ“—÷™÷ĪŌŖy=kx£®k£ĺ0£©”Žňę«ķŌŖ![]() ĹĽ”ŕĶ„A£®x1£¨y1£©£¨B£®x2£¨y2£©ŃĹĶ„£¨‘Úx1y2+x2y1Ķń÷Ķő™°ĺ °Ņ
ĹĽ”ŕĶ„A£®x1£¨y1£©£¨B£®x2£¨y2£©ŃĹĶ„£¨‘Úx1y2+x2y1Ķń÷Ķő™°ĺ °Ņ
A£ģ©Ā6 B£ģ©Ā9 C£ģ0 D£ģ9
°ĺīūįł°ŅA°£
°ĺĹ‚őŲ°Ņ°ŖĶ„A£®x1£¨y1£©£¨B£®x2£¨y2£© «ňę«ķŌŖ![]() …ŌĶńĶ„£¨°ŗx1y1=x2y2=3°£
…ŌĶńĶ„£¨°ŗx1y1=x2y2=3°£
°Ŗ÷ĪŌŖy=kx£®k£ĺ0£©”Žňę«ķŌŖ![]() ĹĽ”ŕĶ„A£®x1£¨y1£©£¨B£®x2£¨y2£©ŃĹĶ„£¨°ŗx1=©Āx2£¨y1=©Āy2
ĹĽ”ŕĶ„A£®x1£¨y1£©£¨B£®x2£¨y2£©ŃĹĶ„£¨°ŗx1=©Āx2£¨y1=©Āy2
°ŗx1y2+x2y1=©Āx1y1©Āx2y2=©Ā3©Ā3=©Ā6°£Ļ —°A°£

Ń∑Ōį≤ŠŌĶŃ–īūįł
 Ĺ›ĺ∂—ĶŃ∑ľž≤‚ĺŪŌĶŃ–īūįł
Ĺ›ĺ∂—ĶŃ∑ľž≤‚ĺŪŌĶŃ–īūįł –°∑Ú◊”»ęń‹ľž≤‚ŌĶŃ–īūįł
–°∑Ú◊”»ęń‹ľž≤‚ŌĶŃ–īūįł
ŌŗĻōŐ‚ńŅ