题目内容
【题目】在平面直角坐标系xOy中,抛物线![]() 与y轴交于点C(0,2),它的顶点为D(1,m),且
与y轴交于点C(0,2),它的顶点为D(1,m),且![]() .
.
(1)求m的值及抛物线的表达式;
(2)将此抛物线向上平移后与x轴正半轴交于点A,与y轴交于点B,且OA=OB.若点A是由原抛物线上的点E平移所得,求点E的坐标;
(3)在(2)的条件下,点P是抛物线对称轴上的一点(位于x轴上方),且∠APB=45°.求P点的坐标.
【答案】(1)![]() (2)E(3,-1)(3)
(2)E(3,-1)(3)![]()
【解析】
(1)作DH⊥y轴,根据![]() ,求出m的值,再根据对称轴是x=1,和C,D两点求出抛物线的表达式即可;
,求出m的值,再根据对称轴是x=1,和C,D两点求出抛物线的表达式即可;
(2)设平移后的抛物线表达式为![]() ,然后得出OA=OB,得出B(0,2+k),A点的坐标为(2+k,0),然后代入求出k的值即可;
,然后得出OA=OB,得出B(0,2+k),A点的坐标为(2+k,0),然后代入求出k的值即可;
(3)设P(1,y),设对称轴与AB的交点为M,与x轴的交点为H,则H(1,0),由(2)得出A,B的坐标,然后得出![]() △BMP∽△BPA,然后根据
△BMP∽△BPA,然后根据![]()
解:(1)作DH⊥y轴,垂足为H,∵D(1,m)(![]() ),∴DH= m,HO=1.
),∴DH= m,HO=1.
∵![]() ,∴
,∴![]() ,∴m=3.
,∴m=3.
∴抛物线![]() 的顶点为D(1,3).
的顶点为D(1,3).
又∵抛物线![]() 与y轴交于点C(0,2),
与y轴交于点C(0,2),
∴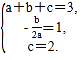 (2∴
(2∴ ∴抛物线的表达式为
∴抛物线的表达式为![]() .
.
(2)∵将此抛物线向上平移,
∴设平移后的抛物线表达式为![]() .
.
则它与y轴交点B(0,2+k).
∵平移后的抛物线与x轴正半轴交于点A,且OA=OB,∴A点的坐标为(2+k,0).
∴![]() .∴
.∴![]() .
.
∵![]() ,∴
,∴![]() .
.
∴A(3,0),抛物线![]() 向上平移了1个单位.
向上平移了1个单位.
∵点A由点E向上平移了1个单位所得,∴E(3,-1).
(3)由(2)得A(3,0),B(0, 3),∴![]() .
.
∵点P是抛物线对称轴上的一点(位于x轴上方),且∠APB=45°,原顶点D(1,3),
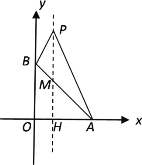
∴设P(1,y),设对称轴与AB的交点为M,与x轴的交点为H,则H(1,0).
∵A(3,0),B(0, 3),∴∠OAB=45°, ∴∠AMH=45°.
∴M(1,2). ∴![]() .
.
∵∠BMP=∠AMH, ∴∠BMP=45°.
∵∠APB=45°, ∴∠BMP=∠APB.
∵∠B=∠B,∴△BMP∽△BPA.
∴![]() .∴
.∴![]()
∴![]() .∴
.∴![]() (舍).
(舍).
∴![]()

【题目】如图有两个边长为4cm的正方形,其中一个正方形的顶点在另一个正方形的中心上,绕着中心旋转其中一个正方形,那么图中阴影部分的面积是( )
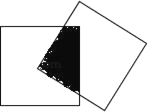
A. 无法确定B. 8cm2C. 16cm2D. 4cm2
【题目】“绿水青山就是金山银山”,为保护生态环境,A,B两村准备各自清理所属区域养鱼网箱和捕鱼网箱,每村参加清理人数及总开支如下表:
村庄 | 清理养鱼网箱人数/人 | 清理捕鱼网箱人数/人 | 总支出/元 |
A | 15 | 9 | 57000 |
B | 10 | 16 | 68000 |
(1)若两村清理同类渔具的人均支出费用一样,求清理养鱼网箱和捕鱼网箱的人均支出费用各是多少元;
(2)在人均支出费用不变的情况下,为节约开支,两村准备抽调40人共同清理养鱼网箱和捕鱼网箱,要使总支出不超过102000元,且清理养鱼网箱人数小于清理捕鱼网箱人数,则有哪几种分配清理人员方案?