Question

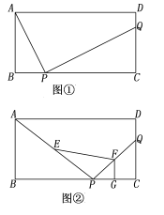
【题目】如图有两个边长为4cm的正方形，其中一个正方形的顶点在另一个正方形的中心上，绕着中心旋转其中一个正方形，那么图中阴影部分的面积是（　　）

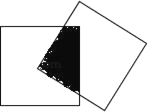
A. 无法确定B. 8cm2C. 16cm2D. 4cm2

Answer 1

【答案】D

【解析】

如图，根据正方形的性质得OD＝OC，∠ODA＝∠OCD＝45°，∠DOC＝90°，再利用等角的余角相等得到∠DOE＝∠COF，于是可根据“ASA”证明△ODE≌△OCF，

则S△ODE＝S△OCF，所以S四边形EOFD＝S△DOC＝S正方形ABCD．

解：如图，

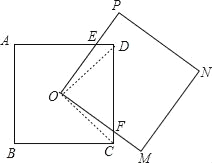
∵四边形ABCD为正方形，

∴OD＝OC，∠ODA＝∠OCD＝45°，∠DOC＝90°，

而∠POM＝90°，

即∠DOF+∠COF＝90°，∠DOE+∠DOF＝90°，

∴∠DOE＝∠COF，

在△ODE和△OCF中，

，

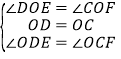∴△ODE≌△OCF（ASA），

∴S△ODE＝S△OCF，

∴S四边形EOFD＝S△DOC＝S正方形ABCD＝×42＝4（cm2）．

故选：D．