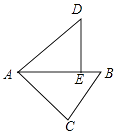题目内容
【题目】如图,已知△ABC是等边三角形,以AC为直径的⊙O分别交AB,BC于点D,E,点F在AB的延长线上,2∠BCF=∠BAC. 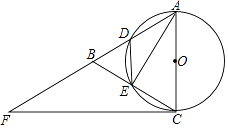
(1)求∠ADE的度数.
(2)求证:直线CF是⊙O的切线.
【答案】
(1)解:∵△ABC是等边三角形,
∴∠ACB=∠ACE=60°,
∴∠ADE=180°﹣∠ACE=120°

(2)解:∵⊙O的直径是AC,
∴∠AEC=90°,即AE⊥BC.
又∵AB=AC,
∴∠BAE=∠CAE.
∵2∠BCF=∠BAC,
∴∠BCF=∠CAE.
∵∠CAE+∠ECA=90°,
∴∠BCF+∠ECA=90°,即∠ACF=90°.
又AC是直径,
∴直线CF是⊙O的切线
【解析】(1)根据圆内接四边形的对角互补可以求得∠ADE的度数.(2)欲证明直线CF是⊙O的切线,只需推知∠ACF=90°.
【考点精析】掌握等边三角形的性质和圆周角定理是解答本题的根本,需要知道等边三角形的三个角都相等并且每个角都是60°;顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半.

练习册系列答案
相关题目
【题目】为了响应市委和市政府“绿色环保,节能减排”的号召,幸福商场用3300元购进甲、乙两种节能灯共计100只,很快售完.这两种节能灯的进价、售价如下表:
进价(元/只) | 售价(元/只) | |
甲种节能灯 | 30 | 40 |
甲种节能灯 | 35 | 50 |
(1)求幸福商场甲、乙两种节能灯各购进了多少只?
(2)全部售完100只节能灯后,商场共计获利多少元?