题目内容
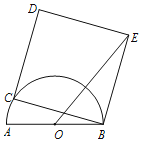
【题目】如图,点C是半圆![]() 上一动点,以BC为边作正方形BCDE,使
上一动点,以BC为边作正方形BCDE,使![]() 在正方形内,连OE,若AB=4cm,则OD的最大值为_____________cm.
在正方形内,连OE,若AB=4cm,则OD的最大值为_____________cm.
【答案】2+2![]() .
.
【解析】
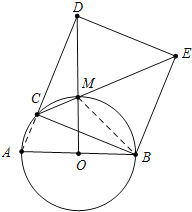
通过旋转观察如图可知当DO⊥AB时,DO最长,设DO与⊙O交于点M,连接CM,先证明△MED≌△MEB,得MD=BM.再利用勾股定理计算即可.
通过旋转观察如图可知当DO⊥AB时,DO最长,设DO与⊙O交于点M,连接CM,
∵∠MCB=![]() ∠MOB=
∠MOB=![]() ×90°=45°,
×90°=45°,
∴∠DCM=∠BCM=45°,
∵四边形BCDE是正方形,
∴C、M、E共线,∠DEM=∠BEM,
在△EMD和△EMB中,
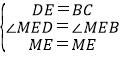 ,
,
∴△MED≌△MEB,(SAS),
∴DM=BM=![]() ,
,
∴OD的最大值=2+2![]() .
.
故答案为:2+2![]() .
.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案
相关题目