题目内容
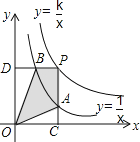
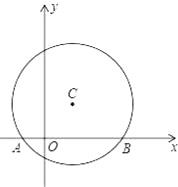
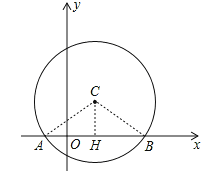
【题目】.如图,在平面直角坐标系中,以点C(1,1)为圆心,2为半径作圆,交x轴于A,B两点,点P在优弧![]() 上.
上.
(1)求出A,B两点的坐标;
(2)试确定经过A、B且以点P为顶点的抛物线解析式;
(3)在该抛物线上是否存在一点D,使线段OP与CD互相平分?若存在,求出点D的坐标;若不存在,请说明理由.
【答案】(1)![]() ,
,![]() (2)
(2)![]() 或
或![]() (3)存在
(3)存在![]() 使线段
使线段![]() 与
与![]() 互相平分
互相平分
【解析】
试题(1)根据垂径定理可得出AH=BH,然后在直角三角形ACH中可求出AH的长,再根据C点的坐标即可得出A、B两点的坐标.
(2)根据抛物线和圆的对称性,即可得出圆心C和P点必在抛物线的对称轴上,因此可得出P点的坐标为(1,3).然后可用顶点式二次函数通式来设抛物线的解析式.根据A或B的坐标即可确定抛物线的解析式.
(3)如果OP、CD互相平分,那么四边形OCPD是平行四边形.因此PC平行且相等于OD,那么D点在y轴上,且坐标为(0,2).然后将D点坐标代入抛物线的解析式中即可判定出是否存在这样的点.
试题解析:(1)如图,作CH⊥AB于点H,连接OA,OB,
∵CH=1,半径CB=2
∴HB=![]() ,
,
故A(1-![]() ,0),B(1+
,0),B(1+![]() ,0).
,0).
(2)由圆与抛物线的对称性可知抛物线的顶点P的坐标为(1,3),
设抛物线解析式y=a(x-1)2+3,
把点B(1+![]() ,0)代入上式,解得a=-1;
,0)代入上式,解得a=-1;
∴y=-x2+2x+2.
(3)假设存在点D使线段OP与CD互相平分,则四边形OCPD是平行四边形
∴PC∥OD且PC=OD.
∵PC∥y轴,
∴点D在y轴上.
又∵PC=2,
∴OD=2,即D(0,2).
又D(0,2)满足y=-x2+2x+2,
∴点D在抛物线上
∴存在D(0,2)使线段OP与CD互相平分.

练习册系列答案
相关题目