题目内容
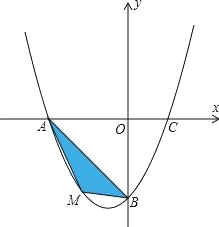
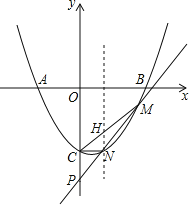
【题目】已知二次函数y=ax2+bx+c的图象对称轴为x=
，图象交x轴于A，B，交y轴于C（0，-3），且AB=5，直线y=kx+b（k＞0）与二次函数图象交于M，N（M在N的右边），交y轴于P．
（1）求二次函数图象的解析式；
（2）若b=-5，且△CMN的面积为3，求k的值；
（3）若b=-3k，直线AN交y轴于Q，求
的值或取值范围．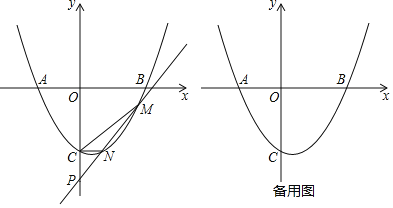
【答案】（1）
；（2）k=2；（3）
≥
.
【解析】
（1）由图象对称轴为x=
，AB=5，知：A（-2，0）、B（0，-3），把A、B、C点坐标代入二次函数即可求解；
（2）S△CMN=HNxM=6，用根与系数的关系求解即可；
（3）求出xN=
，分2k-5＞0时和2k-5＜0两种情况，求出点Q坐标即可求解．
（1）由图象对称轴为x=，AB=5，知：A（-2，0）、B（0，-3），
把A、B、C点坐标代入二次函数表达式得：a=，b=-，c=-3；
故函数表达式为：y=x2-x-3…①；
（2）b=-5，直线MN表达式为：y=kx-5…②，
设：M（x1，y1），N（x2，y2），
将①、②联立并整理得：x2-（2k+1）x+4=0，
则：x1+x2=2k+1，x1x2=4，
直线C（0，-3）、M（x1，y1）所在的直线方程为：
y=
，
过N点做直线HM∥y轴，交MC于H，则H（x1，
x13），
S△CMN=HNxM=6，
整理得：x1y2-x2y1+3x1-3x2=6，
把y1=3x1-5，y2=3x2-5，代入上式整理得：
x2-x1=3，
即：（x1+x2）2-4x1x2=9，
k=2；
（3）b=-3k，直线y=kx+b=kx-3k…③，
将①、③方程联立并整理得：
x2-（2k+1）x+（6k-6）=0，
△=4k2-20k+25=（2k-5）2＞0，
xN=，
当2k-5＞0时，
xN=3，则N（3，0），
而Q（0，0），P（0，-3k），C（0，-3）
则：CP=3k-3，CQ=3，
∴=k-1，即：＞；
当2k-5＜0时，
xN=2k-2，则N（2k-2，2k2-5k），
则AN所在的直线方程为：y=
x+(2k5)，
则：Q（0，2k-5），
而C（0，-3）P（0，-3k），
则：CP=3k-3，CQ=2k-2，
∴=，
故：≥．
