��Ŀ����
ijˮ������������ÿ�����Ϊ40Ԫ��ƻ������۲��Ź涨ÿ���ۼ۲��ø���55Ԫ���г����鷢�֣���ÿ����50Ԫ�ļ۸����ۣ�ƽ��ÿ������90�䣬�۸�ÿ���1Ԫ��ƽ��ÿ��������3�䣮
��1����ƽ��ÿ�������� �������ۼ�
�������ۼ� Ԫ/��֮��ĺ�����ϵʽ��
Ԫ/��֮��ĺ�����ϵʽ��
��2�����������ƽ��ÿ�����������w��Ԫ�������ۼ� ��Ԫ/�䣩֮��ĺ�����ϵʽ��
��Ԫ/�䣩֮��ĺ�����ϵʽ��
��3����ÿ��ƻ�������ۼ�Ϊ����Ԫʱ�����Ի�����������������Ƕ��٣�
��1�� ����2��
����2�� ����3��55��1125��
����3��55��1125��
�������������������ͨ����������ģ�ͽ��������������⣮���������ó�ƽ��ÿ����������y�������ۼ�x��Ԫ/�䣩֮��ĺ�����ϵʽΪ ��Ȼ�������������=�����������ۼ۩����ۣ����г�ƽ��ÿ�����������w��Ԫ�������ۼ�x��Ԫ/�䣩֮��ĺ�����ϵʽ�������ݺ���������������������
��Ȼ�������������=�����������ۼ۩����ۣ����г�ƽ��ÿ�����������w��Ԫ�������ۼ�x��Ԫ/�䣩֮��ĺ�����ϵʽ�������ݺ���������������������
�����������1��������ã� ������ã�
������ã� ��
��
��2��������ã� ��
��
��3�� ����
���� ���������߿������£���
���������߿������£��� ʱ��w�����ֵ����
ʱ��w�����ֵ���� ��w��x����������൱
��w��x����������൱ Ԫʱ��w�����ֵΪ1125Ԫ���൱ÿ��ƻ�������ۼ�Ϊ55Ԫʱ�����Ի��1125Ԫ���������
Ԫʱ��w�����ֵΪ1125Ԫ���൱ÿ��ƻ�������ۼ�Ϊ55Ԫʱ�����Ի��1125Ԫ���������
���㣺���κ�����Ӧ�ã�

��ϰ��ϵ�д�
 ��Ч���ܿ�ʱ��ҵϵ�д�
��Ч���ܿ�ʱ��ҵϵ�д� �ݾ�ѵ������ϵ�д�
�ݾ�ѵ������ϵ�д�
�����Ŀ
 �Ķ���������
�Ķ��������� 
 �ĸ���
�ĸ��� ��
�� ��
�� ����CD=3��
����CD=3�� ��ͼ���ϣ���k=��1��
��ͼ���ϣ���k=��1��

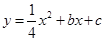 ��x�ύ�ڵ�A��B����A�ڵ�B�Ҳࣩ����y�ύ�ڵ�C(0��-3)����OA=2OC��
��x�ύ�ڵ�A��B����A�ڵ�B�Ҳࣩ����y�ύ�ڵ�C(0��-3)����OA=2OC�� ��ֵ��
��ֵ�� x2��Ӧ�ĵ���Ϊ�� ����������y=4x2��Ӧ�ĵ���Ϊ�� ����������y=ax2��a��0����Ӧ�ĵ���Ϊ������������y=a��x��2��2+3��a��0����Ӧ�ĵ���Ϊ������
x2��Ӧ�ĵ���Ϊ�� ����������y=4x2��Ӧ�ĵ���Ϊ�� ����������y=ax2��a��0����Ӧ�ĵ���Ϊ������������y=a��x��2��2+3��a��0����Ӧ�ĵ���Ϊ������ ��a��0����Ӧ�ĵ���Ϊ6������x���ϣ���a��ֵ��
��a��0����Ӧ�ĵ���Ϊ6������x���ϣ���a��ֵ��