题目内容
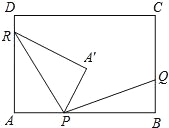
【题目】如图，已知，EG∥AF，请你从下面三个条件中，再选出两个作为已知条件，另一个作为结论，推出一个正确的命题。并证明这个命题（只写出一种情况）①AB=AC; ②DE=DF; ③BE=CF。（在已知和求证中，填写正确序号）
已知：EG∥AF,_______,_________.
求证：__________.
【答案】答案不唯一.
【解析】试题分析：选择AB=AC，DE=DF，求证BE=CF，要证BE=CF，需证EG=CF，即需证△DEG≌△DFC，由已知可证BE=EG．和△DEG≌△DFC，所以EG=CF，即证BE=CF．（根据三角形全等的判定定理可选）①③②，即已知：EG∥AF，AB=AC，BE=CF．求证：DE=DF．
试题解析：已知：EG∥AF，AB=AC，DE=DF．
求证：BE=CF．
证明：∵EG∥AF，
∴∠GED=∠F，∠BGE=∠BCA，
∵AB=AC，
∴∠B=∠BCA，
∴∠B=∠BGE，
∴BE=EG．
∵DE=DF，
∴△DEG≌△DFC，
∴EG=CF，
∴BE=CF．
练习册系列答案
教材全解字词句篇系列答案
相关题目
【题目】根据国家发改委实施“阶梯电价”的有关文件要求，某市结合地方实际，决定对居民生活用电实行“阶梯电价”收费，具体收费标准见表：
一户居民一个月用电量的范围 | 电费价格（单位：元/度） |
不超过200度 | a |
超过200度的部分 | b |
已知4月份，该市居民甲用电250度，交电费130元；居民乙用电400度，交电费220元．
（1）求出表中a和b的值；
（2）实行“阶梯电价”收费以后，该市一户居民月用电多少度时，其当月的平均电价每度不超过0.56元？
