题目内容
【题目】已知二次函数 y＝（x－a－2）（x+a）+3．
（1）求该二次函数的图象的对称轴．
（2）对于该二次函数图象上的两点 P（x1，y1）、Q（x2，y2）．
①当 x≥m 时，y 随 x 的增大而增大，写出一个符合条件的 m 值；
②当 m≤x2≤m+2，当 x1≤﹣1 时，均有 y1≥y2，求 m 的取值范围；
（3）当二次函数过（0，3）点时，且与直线 y=kx+2 交于 A、B 两点，其中有一交点的横坐标 x0 满足 1＜x0＜3， 求 k 的取值范围．
【答案】（1）x=1；（2）①m值可以为2；②-1≤m≤1；（3）
【解析】
（1）首先把原二次函数化成y=（x-1）2-a2-2a+2，由此可得该二次函数的图象的对称轴；
（2）①根据二次函数的开口方向和对称轴可知y随x的增大而增大时，x的取值范围，从而可得符合条件的m值；
②首先得出当x1=-1，y1=y2时，x2=3，然后根据当x1≤-1时，均有y1≥y2，可得一个不等式组，解出即可；
（3）首先根据二次函数过（0，3）点，求出a的值，于是可得该二次函数的解析式，然后计算出直线x=1，直线x=3与二次函数y=x2-2x+3的交点坐标，得到直线DE的解析式为y=2，k1=0，设DF所在直线解析式为y=k2x+2，把（3，6）代入得k2=
即可得出结论.
解：（1）因为y=（x-a-2）（x+a）+3，
∴y=（x-1）2-a2-2a+2，
∴该二次函数的图象的对称轴为x=1；
（2）①∵该二次函数开口向上，对称轴为x=1，
∴x≥1时，y随x的增大而增大，
∴m≥1的数都可以，
因此符合条件的m值可以为2；
②∵该二次函数的图象的对称轴为x=1，
∴当x1=-1，y1=y2时，x2=3，
∴当x1≤-1时，均有y1≥y2，
则-1≤x2≤3，
∴
，
解得-1≤m≤1；
（3）当二次函数过（0，3）点时，
则有3=（0-1）2-a2-2a+2，
解得a=0或-2，
∴该二次函数的解析式为y=x2-2x+3，
如图：
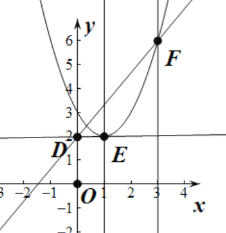
直线x=1，直线x=3分别与二次函数y=x2-2x+3交E、F两点，
易得E（1，2），F（3，6），
直线y=kx+2与y轴交于D点，D（0，2），
∵二次函数y=x2-2x+3与直线y=kx+2交于A、B两点，其中有一交点的横坐标
满足1＜x0＜3，
直线y=kx+2与二次函数y=x2-2x+3的EF间有一交点，
直线DE的解析式为y=2，k1=0，设DF所在直线的解析式为y=k2x+2，把（3，6）代入得k2=，
∴k1<k<k2，即.
