题目内容
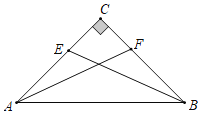
【题目】如图，等腰直角△ABC中，∠C=90°，AC=BC=
，E、F为边AC、BC上的两个动点，且CF=AE，连接BE、AF，则BE+AF的最小值为_____．
【答案】2
．
【解析】
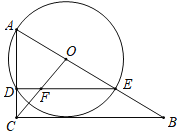
如图，作点C关于直线B的对称点D，连接AD，BD，延长DA到H，使得AH=AD，连接EH，BH，DE．想办法证明AF=DE=EH，BE+AF的最小值转化为EH+EB的最小值．
如图，作点C关于直线B的对称点D，连接AD，BD，延长DA到H，使得AH=AD，连接EH，BH，DE．
∵CA=CB，∠C=90°，
∴∠CAB=∠CBA=45°，
∵C，D关于AB对称，
∴DA=DB，∠DAB=∠CAB=45°，∠ABD=∠ABC=45°，
∴∠CAD=∠CBD=∠ADC=∠C=90°，
∴四边形ACBD是矩形，
∵CA=CB，
∴四边形ACBD是正方形，
∵CF=AE，CA=DA，∠C=∠EAD=90°，
∴△ACF≌△DAE（SAS），
∴AF=DE，
∴AF+BE=ED+EB，
∵CA垂直平分线段DH，
∴ED=EH，
∴AF+BE=EB+EH，
∵EB+EH≥BH，
∴AF+BE的最小值为线段BH的长，BH=
，
∴AF+BE的最小值为2，
故答案为：2．
练习册系列答案
走进文言文系列答案
相关题目
