Question

【题目】如图，△ABC是等边三角形，点D在AC上，点E在BC的延长线上，且BD＝DE.

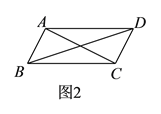
（1）若点D是AC的中点，如图1，求证：AD＝CE

（2）若点D不是AC的中点，如图2，试判断AD与CE的数量关系，并证明你的结论：（提示：过点D作DF∥BC，交AB于点F）

Answer 1

【答案】（1）证明见解析；（2）AD=CE，证明见解析.

【解析】分析：（1）求出∠E=∠CDE，推出CD=CE，根据等腰三角形性质求出AD=DC，即可得出答案；（2）过D作DF∥BC，交AB于F，证△BFD≌△DCE，推出DF=CE，证△ADF是等边三角形，推出AD=DF，即可得出答案．

本题解析：

（1）证明：∵△ABC是等边三角形，∴∠ABC=∠ACB=60°，AB=AC=BC，∵D为AC中点，∴∠DBC=30°，AD=DC，∵BD=DE，∴∠E=∠DBC=30°∵∠ACB=∠E+∠CDE，

∴∠CDE=30°=∠E，∴CD=CE，∵AD=DC，∴AD=CE；

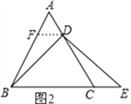
（2）AD=CE，如图2，过D作DF∥BC，交AB于F，

则∠ADF=∠ACB=60°，∵∠A=60°，∴△AFD是等边三角形，

∴AD=DF=AF，∠AFD=60°，∴∠BFD=∠DCE=180°﹣60°=120°，

∵DF∥BC，∴∠FDB=∠DBE=∠E，

在△BFD和△DCE中，∴△BFD≌△DCE，∴CE=DF=AD，即AD=CE．