题目内容
如图，在等腰梯形ABCD中，AD∥BC，∠C＝60°，AD＝CD．E、F分别在AD、CD上，DE＝CF，AF、BE交于点P．
⑴试说明：AF=BE ⑵猜测∠BPF的度数，并说明你的结论的正确性．
⑴试说明：AF=BE ⑵猜测∠BPF的度数，并说明你的结论的正确性．
⑴ 证△ABE≌△ADF得AF=BE ⑵ ∠BPF=120o
(1)通过SAS证明△ABE≌△DAF，即得AF=BE;
(2)由△ABE≌△DAF可知∠BPF=∠ABP+∠PAB=∠DAF+∠PAB=∠EAB，又∠C=60°，可知∠EAB=120°，继而即可求出的答案．
(2)由△ABE≌△DAF可知∠BPF=∠ABP+∠PAB=∠DAF+∠PAB=∠EAB，又∠C=60°，可知∠EAB=120°，继而即可求出的答案．
练习册系列答案
高效智能课时作业系列答案
捷径训练检测卷系列答案
相关题目
; 
; 
.
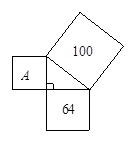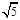