题目内容
如图,在△ABC中,AD⊥BC,垂足为D,E、F分别是AB、AC的中点.

⑴若∠C=70°,求∠AFD的度数
⑵当△ABC满足什么条件时,四边形AEDF为菱形?为什么?
⑶在⑵的基础上,△ABC还需满足什么条件才能使四边形AEDF为正方形?为什么?

⑴若∠C=70°,求∠AFD的度数
⑵当△ABC满足什么条件时,四边形AEDF为菱形?为什么?
⑶在⑵的基础上,△ABC还需满足什么条件才能使四边形AEDF为正方形?为什么?
(1)140°(2)AB=AC,证明略 (3)AB=AC且∠BAC=90°,证明略
(1)由AD垂直于BC,根据垂直定义得到∠ADC=90°,即三角形ADC为直角三角形,又F为AC的中点,根据斜边上的中线等于斜边的一半,可得DF等于AC的一半,再根据中点定义得到AF与CF相等,且都等于AC的一半,等量代换可得DF=CF,根据等边对等角得到∠FDC=∠C,由∠C的度数求出∠FDC的度数,由∠AFD为三角形FDC的外角,根据外角性质即可求出所求角的度数;
(2)三角形ABC满足AB=AC时,四边形AEDF为菱形,理由为:由AB=AC,且AD与BC垂直,根据三线合一得到D为BC的中点,又F为中点,可得DF为三角形ABC的中位线,可得DF与AB平行,且等于AB的一半,又AE也为AB的一半,等量代换可得AE=DF,又AE与DF平行,根据一组对边平行且相等的四边形为平行四边形,再由DE也为三角形ABC的中位线,可得ED等于AC的一半,由AB=AC,等量代换可得DE=DF,根据邻边相等的平行四边形为菱形可得AEDF为菱形;
(3)由第二问三角形ABC满足AB=AC,得到AEDF为菱形,再加上∠BAC=90°,根据有一个角为直角的菱形为正方形可得AEDF为正方形.
(2)三角形ABC满足AB=AC时,四边形AEDF为菱形,理由为:由AB=AC,且AD与BC垂直,根据三线合一得到D为BC的中点,又F为中点,可得DF为三角形ABC的中位线,可得DF与AB平行,且等于AB的一半,又AE也为AB的一半,等量代换可得AE=DF,又AE与DF平行,根据一组对边平行且相等的四边形为平行四边形,再由DE也为三角形ABC的中位线,可得ED等于AC的一半,由AB=AC,等量代换可得DE=DF,根据邻边相等的平行四边形为菱形可得AEDF为菱形;
(3)由第二问三角形ABC满足AB=AC,得到AEDF为菱形,再加上∠BAC=90°,根据有一个角为直角的菱形为正方形可得AEDF为正方形.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目

 ”型甬道,甬道宽度相等,甬道面积是整个梯形面积的
”型甬道,甬道宽度相等,甬道面积是整个梯形面积的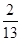 .设甬道的宽为
.设甬道的宽为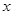 米.
米.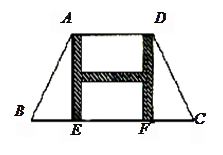
 的周长;
的周长; 

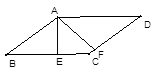
 ,
, ,圆A与圆C交于B、D两点),连结AB、BC、CD、DA.若能作出满足要求的四边形ABCD,则
,圆A与圆C交于B、D两点),连结AB、BC、CD、DA.若能作出满足要求的四边形ABCD,则 应满足什么条件?
应满足什么条件? ,求四边形ABCD的面积.
,求四边形ABCD的面积. 的矩形,接着把其中一个面积为
的矩形,接着把其中一个面积为 的矩形,再把其中一个面积为
的矩形,再把其中一个面积为 的矩形,如此进行下去,试利用图形所揭示的规律计算:
的矩形,如此进行下去,试利用图形所揭示的规律计算:
 .
.