题目内容
【题目】四边形ABCD是正方形，点E是直线AB上的一动点，且△AEC是以AC为腰的等腰三角形，则∠BCE的度数为_____．
【答案】67.5°或45°或22.5°
【解析】分析：由于没有说明△AEC的顶点，所以分情况进行讨论．
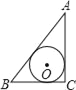
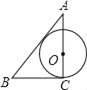
详解：如图，
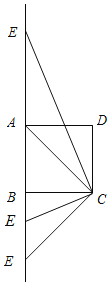
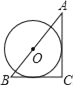
当AC=AE时，
以A为圆心，AC为半径作圆交直线AB于点E，
当E在BA的延长线时，
∴∠EAC=135°，
∴∠BEC=22.5°，
∴∠BCE=∠BCA+∠BEC=67.5°
当E在AB的延长线时，
∴∠EAC=45°，
∴∠ACE=67.5°
∴∠BCE=∠ACE-∠ACB=22.5°
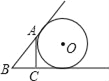
当AC=CE时，
当以C为圆心AC为半径作圆交直线AB于点E
∴∠EAC=∠CEA=45°，
∴∠BCE=45°，
故答案为：67.5°或45°或22.5°
练习册系列答案
名校课堂系列答案
相关题目
