题目内容
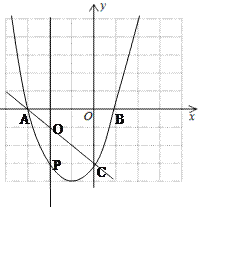
【题目】如图所示,一次函数![]() 分别交x,y轴于A,C两点,抛物线
分别交x,y轴于A,C两点,抛物线![]() 与经过点A,C.
与经过点A,C.
(1)求此抛物线的函数表达式;
(2)若P为抛物线上A,C两点间的一个动点,过点P作直线![]() ,交直线AC于点Q,当点P运动到什么位置时,线段PQ的长度最大?求此最大长度,及此时P点坐标。
,交直线AC于点Q,当点P运动到什么位置时,线段PQ的长度最大?求此最大长度,及此时P点坐标。
(3)在(2)条件下,直线![]() 与
与![]() 轴交于N点与直线AC交于点M,当N,M,Q,D四点是平行四边行时,直接写出D点的坐标。
轴交于N点与直线AC交于点M,当N,M,Q,D四点是平行四边行时,直接写出D点的坐标。

【答案】(1)![]() ;(2)当
;(2)当![]() 时,PQ最大=
时,PQ最大=![]() , P(
, P(![]() );
);
(3)![]()
![]()
![]() .
.
【解析】试题分析: (1)先求出A、C坐标,把A、C两点坐标代入y=x+bx+c解方程组即可.
(2)设P(a,a+2a3),则Q(a,a3),构建二次函数,利用二次函数的性质解决问题.
(3)如图2中,分两种情形①当MN为平行四边形的边时,DQ=MN=2,可得D1(![]() ,
, ![]() ),D2(
),D2(![]() ,
,![]() ).②当MN为对角线时,可得D3(
).②当MN为对角线时,可得D3(![]() ,
,![]() ).
).
试题解析: (1)∵一次函数y=x3分别交x,y轴于A,C两点,
∴A(3,0)C(0,3),把A、C两点坐标代入y=x+bx+c
得![]()
解得![]() ,
,
∴y=x +2x3.
(2)设P(a,a +2a3),则Q(a,a3),
∴PQ=a3(a +2a3)=a 3a=(a![]() )+
)+![]() .
.
∴当a=![]() 时,PQ是最大值=
时,PQ是最大值=![]() ,
,
此时P(![]() ,
,![]() ).
).
(3)如图2中,
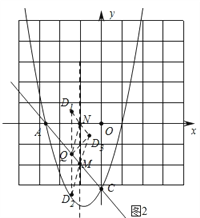
∵N(1,0),M(1,2),Q(![]() ,
,![]() ),
),
∴MN=2,
①当MN为平行四边形的边时,DQ=MN=2,
∴![]() ,
, ![]() .
.
②当MN为对角线时,可得![]() ,
,
综上所述,满足条件的点D的坐标为![]()
![]()
![]() .
.
点睛: 本题考查二次函数、一次函数的应用、最值问题、平行四边形的判定和性质等知识,解题的关键是学会构建二次函数解决最值问题,学会分类讨论的思想思考问题,属于中考常考题型.

练习册系列答案
相关题目