��Ŀ����
����Ŀ����ͼ,��ƽ��ֱ������ϵ��,Rt��ABC����������ֱ���A(-3,2),B(0,4),C(0,2).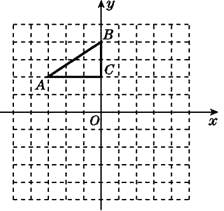
��1������ABC�Ե�CΪ��ת������ת180��,������ת���Ӧ�ġ�A1B1C;ƽ�ơ�ABC,����A�Ķ�Ӧ��A2������Ϊ(0,-4),����ƽ�ƺ��Ӧ�ġ�A2B2C2.
��2��������A1B1C��ijһ����ת���Եõ���A2B2C2,��ֱ��д����ת���ĵ�����.
��3����x������һ��P,ʹ��PA+PB��ֵ��С,��ֱ��д����P������.
���𰸡�
��1���⣺��ͼ��ʾ.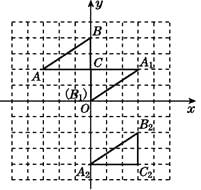
��2���⣺��ͼ������A1A2 �� CC2 �� A1A2��CC2�ཻ�ڵ�P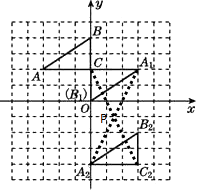
��ת���ĵ�����Ϊ��P��
A1��3,2����A2��0��-4��
��ֱ��A1A2�Ľ���ʽΪy1=kx+b![]() ,��֮�ã�
,��֮�ã�![]()
y1=2x-4
C��0,2����C2��3��-4��
��ֱ��CC2�Ľ���ʽΪy2=mx+n
��![]() ,��֮�ã�
,��֮�ã�![]()
��y2=-2x+2
��y1=y2
��2x-4=-2x+2
x=![]() ��y2=-1
��y2=-1
��P��![]() ��-1��
��-1��
����ת���ĵ�������P��![]() ��-1��
��-1��
��3���⣺��ͼ������A����x��ĶԳƵ�M������BM��x���ڵ�N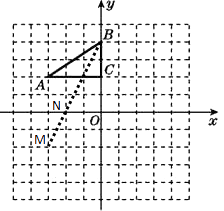
��M��-3��-2����B��0,4��
��ֱ��MB�Ľ���ʽΪy=kx+b![]() ,��֮�أ�
,��֮�أ�![]()
y=2x+4
y=0ʱ��2x+4=0����x=-2
�ʵ�P������Ϊ(-2,0)
����������1����������ṹ�ҳ���A��B��C��ת180���Ķ�Ӧ��A1��B1��C1��λ�ã�Ȼ��˳�����Ӽ��ɣ��ҳ�ƽ�ƺ�Ķ�Ӧ��A2��B2��C2��λ�ã�Ȼ��˳�����Ӽ��ɡ�
��2��������ת�Ķ�����ͼ�Σ�����A1A2 �� CC2 �� A1A2��CC2�ཻ�ڵ�P�������ֱ��A1A2��ֱ��CC2�ĺ�������ʽ��������������Ľ������꣬������ת���ĵ�P�����ꡣ
��2������A����x��ĶԳƵ�M������BM��x���ڵ�N�����ô���ϵ�������ֱ��MB�Ľ���ʽ���ٸ���y=0�������ɵó�P�����ꡣ