题目内容
【题目】如图9,已知在等边三角形ABC中,D是AC的中点,E为BC延长线上一点,且CE=CD,DM ![]() BC,垂足为M.求证:M是BE的中点.
BC,垂足为M.求证:M是BE的中点.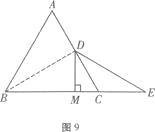
【答案】证明: ![]()
![]() ,
,![]() ,
,![]()
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
【解析】根据等边三角形的性质得出B D 平 分 ∠ A B C , ∠ A B C = ∠ A C B = 6 0 ° ,进而根据角平分线的定义得出∠ D B C = 3 0 ° ,根据三角形外角的定理及等边对等角得出∠ C D E = ∠ E = 3 0 ° ,根据等量代换得出∠ D B C = ∠ E ,根据等角对等边得出B D = D E ,根据等腰三角形的三线合一得出M是BE的中点。
【考点精析】根据题目的已知条件,利用三角形的外角和等边三角形的性质的相关知识可以得到问题的答案,需要掌握三角形一边与另一边的延长线组成的角,叫三角形的外角;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角;等边三角形的三个角都相等并且每个角都是60°.

练习册系列答案
相关题目