题目内容
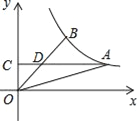
【题目】如图,在△OAB中,OA=OB,C为AB中点,以O为圆心,OC长为半径作圆,AO与⊙O交于点E,直线OB与⊙O交于点F和D,连接EF、CF与OA交于点G.
(1)求证:直线AB是⊙O的切线;
(2)求证:ODEG=OGEF;
(3)若AB=8,BD=2,求⊙O的半径.

【答案】(1)(2)见解析 (3)3.
【解析】(1)利用等腰三角形的性质,证明OC⊥AB即可;
(2)证明OC∥EG,推出△GOC∽△GEF即可解决问题;
(3)设OC=OD=r,在Rt△BOC中,根据OB2=OC2+BC2,列出方程即可解决问题;
(1)证明:∵OA=OB,AC=BC,
∴OC⊥AB,
∴⊙O是AB的切线.
(2)证明:∵OA=OB,AC=BC,
∴∠AOC=∠BOC,
∵OE=OF,
∴∠OFE=∠OEF,
∵∠AOB=∠OFE+∠OEF,
∴∠AOC=∠OEF,
∴OC∥EF,
∴△GOC∽△GEF,
∴![]() =
=![]() ,∵OD=OC,
,∵OD=OC,
∴ODEG=OGEF.
(3)解:设OC=OD=r,
在Rt△BOC中,∵OB2=OC2+BC2,
∴(r+2)2=r2+42,
∴r=3,
∴⊙O的半径为3.


练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目