题目内容
【题目】已知,点![]() 为二次函数
为二次函数![]() 图象的顶点,直线
图象的顶点,直线![]() 分别交
分别交![]() 轴正半轴,
轴正半轴,![]() 轴于点
轴于点![]() .
.
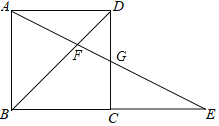
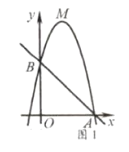
(1)如图1,若二次函数图象也经过点![]() ,试求出该二次函数解析式,并求出
,试求出该二次函数解析式,并求出![]() 的值.
的值.
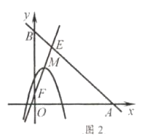
(2)如图2,点![]() 坐标为
坐标为![]() ,点
,点![]() 在
在![]() 内,若点
内,若点![]() ,
,![]() 都在二次函数图象上,试比较
都在二次函数图象上,试比较![]() 与
与![]() 的大小.
的大小.
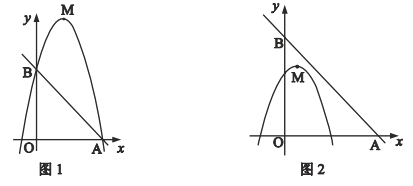
【答案】(1)![]() ,
,![]() ;(2)①当
;(2)①当![]() 时,
时,![]() ;②当
;②当![]() 时,
时,![]() ;③当
;③当![]() 时,
时,![]()
【解析】
(1)根据一次函数表达式求出B点坐标,然后根据B点在抛物线上,求出b值,从而得到二次函数表达式,再根据二次函数表达式求出A点的坐标,最后代入一次函数求出m值.(2)根据解方程组,可得顶点M的纵坐标的范围,根据二次函数的性质,可得答案.
(1)如图1,∵直线![]() 与
与![]() 轴交于点为
轴交于点为![]() ,∴点
,∴点![]() 坐标为
坐标为![]()
又∵![]() 在抛物线上,∴
在抛物线上,∴![]() ,解得
,解得![]()
∴二次函数的表达式为![]()
∴当![]() 时,得
时,得![]() ,
,![]()
∴![]()
代入![]() 得,
得,![]() ,∴
,∴![]()
(2)如图2,根据题意,抛物线的顶点![]() 为
为![]() ,即
,即![]() 点始终在直线
点始终在直线![]() 上,
上,
∵直线![]() 与直线
与直线![]() 交于点
交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,而直线
,而直线![]() 表达式为
表达式为![]()
解方程组![]() ,得
,得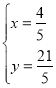
∴点![]() ,
,![]()
∵点![]() 在
在![]() 内,∴
内,∴![]()
当点![]() 关于抛物线对称轴(直线
关于抛物线对称轴(直线![]() )对称时,
)对称时,![]() ,∴
,∴![]()
且二次函数图象的开口向下,顶点![]() 在直线
在直线![]() 上
上
综上:①当![]() 时,
时,![]() ;②当
;②当![]() 时,
时,![]() ;③当
;③当![]() 时,
时,![]() .
.

 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
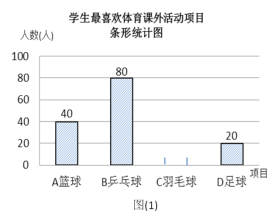
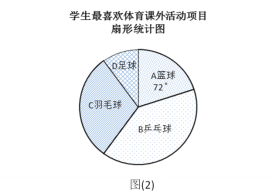
金状元绩优好卷系列答案【题目】电子政务、数字经济、智慧社会一场数字革命正在神州大地激荡.在第二届数字中国建设峰会召开之际,某校举行了第二届“掌握新技术,走进数时代”信息技术应用大赛,将该校八年级参加竞赛的学生成绩统计后,绘制成如下统计图表(不完整):
“掌握新技术,走进数时代”信息技术应用大赛成绩频数分布统计表
组别 | 成绩x(分) | 人数 |
A | 60≤x<70 | 10 |
B | 70≤x<80 | m |
C | 80≤x<90 | 16 |
D | 90≤x≤100 | 4 |
请观察上面的图表,解答下列问题:
(1)统计表中m= ;统计图中n= ,D组的圆心角是 度.
(2)D组的4名学生中,有2名男生和2名女生.从D组随机抽取2名学生参加5G体验活动,请你画出树状图或用列表法求:
①恰好1名男生和1名女生被抽取参加5G体验活动的概率;
②至少1名女生被抽取参加5G体验活动的概率.