题目内容
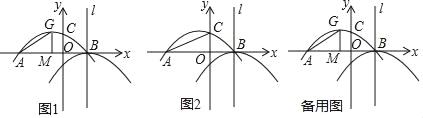
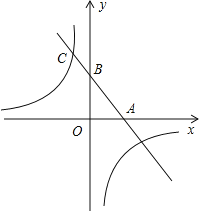
【题目】如图,一次函数y=kx+b的图象与x轴,y轴分别相交于A,B两点,且与反比例函数y=﹣![]() 的图象在第二象限交与点C,如果点A为的坐标为(2,0),B是AC的中点.
的图象在第二象限交与点C,如果点A为的坐标为(2,0),B是AC的中点.
(1)求点C的坐标及k、b的值.
(2)求出一次函数图象与反比例函数图象的另一个交点的坐标,并直接写出当![]() 时,x的取值范围.
时,x的取值范围.
【答案】(1)C(﹣2,4);![]() ;(2)另一个交点坐标为(4,﹣2),x的取值范围为x<﹣2或0<x<4.
;(2)另一个交点坐标为(4,﹣2),x的取值范围为x<﹣2或0<x<4.
【解析】
(1)由A(2,0)利用平行线等分线段定理,可求出点C的横坐标,代入反比例函数关系式,可求其纵坐标;用两点法确定一次函数的关系式,即待定系数法确定函数的关系式,求出k、b的值;
(2)可将两个函数的关系式联立成方程组,解出方程组的解,若有两组解,说明两个函数的图象有两个交点,根据图象可以直观看出一次函数值大于反比例函数值时,自变量的取值范围.
(1)过点C作CD⊥x轴,垂足为D,
∵CD∥OB,
∴![]() ,
,
又∵B是AC的中点.
∴AB=BC,
∴OA=OD
∵A(2,0),
∴OA=OD=2,
当x=﹣2时,y=﹣![]() =4,
=4,
∴C(﹣2,4)
把A(2,0),C(﹣2,4)代入y=kx+b得:
![]() 解得:
解得:![]() ,
,
∴一次函数的关系式为:y=﹣x+2;
因此:C(﹣2,4),k=﹣1,b=2.
(2)由题意得:
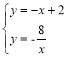 解得:
解得:![]() ;
;
∵一个交点C(﹣2.4)
∴另一个交点E(4,﹣2);
当![]() 时,即:y一次函数>y反比例函数,
时,即:y一次函数>y反比例函数,
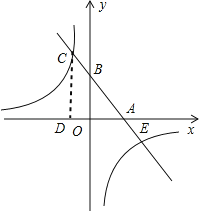
由图象可以直观看出自变量x的取值范围:x<﹣2或0<x<4.
因此:另一个交点坐标为(4,﹣2),x的取值范围为x<﹣2或0<x<4.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目