题目内容
【题目】已知⊙O的直径为10,点A,点B,点C在⊙O上,∠CAB的平分线交⊙O于点D.

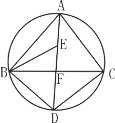
(1)如图①,若BC为⊙O的直径,AB=6,求AC,BD,CD的长;
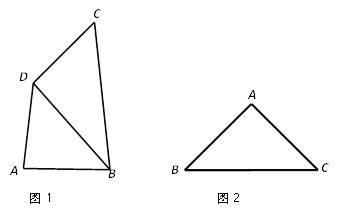
(2)如图②,若∠CAB=60°,求BD的长.
【答案】(1)8;5![]() ;5
;5![]() ;(2)5.
;(2)5.
【解析】
试题(1)利用圆周角定理可以判定△CAB和△DCB是直角三角形,利用勾股定理可以求得AC的长度;利用圆心角、弧、弦的关系推知△DCB也是等腰三角形,所以利用勾股定理同样得到BD=CD=5![]() ;
;
(2)如图②,连接OB,OD.由圆周角定理、角平分线的性质以及等边三角形的判定推知△OBD是等边三角形,则BD=OB=OD=5.
试题解析:(1)如图①,
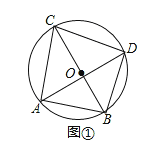
∵BC是⊙O的直径,
∴∠CAB=∠BDC=90°.
∵在直角△CAB中,BC=10,AB=6,
∴由勾股定理得到:AC=![]() .
.
∵AD平分∠CAB,
∴![]() ,
,
∴CD=BD.
在直角△BDC中,BC=10,CD2+BD2=BC2,
∴易求BD=CD=5![]() ;
;
(2)如图②,连接OB,OD.
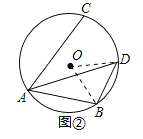
∵AD平分∠CAB,且∠CAB=60°,
∴∠DAB=![]() ∠CAB=30°,
∠CAB=30°,
∴∠DOB=2∠DAB=60°.
又∵OB=OD,
∴△OBD是等边三角形,
∴BD=OB=OD.
∵⊙O的直径为10,则OB=5,
∴BD=5.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
【题目】若二次函数y=ax2+bx+c的x与y的部分对应值如下表:则下列说法错误的是( )
x | … | -1 | 0 | 1 | 2 | 3 | … |
y | … |
|
|
|
|
| … |
A. 二次函数图像与x轴交点有两个
B. x≥2时y随x的增大而增大
C. 二次函数图像与x轴交点横坐标一个在-1~0之间,另一个在2~3之间
D. 对称轴为直线x=1.5