题目内容
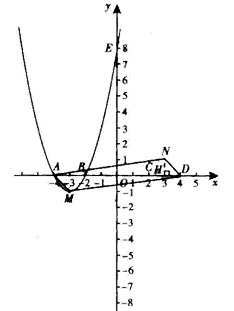
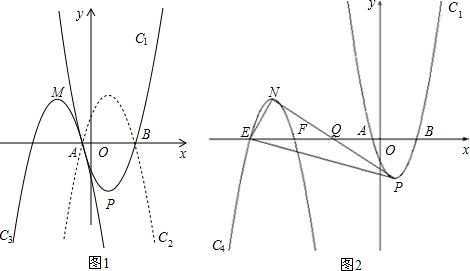
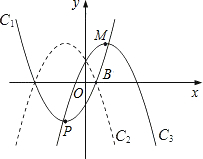
如图,已知抛物线C1与坐标轴的交点依次是A(-4,0),B(-2,0),E(0,8)。
(1)求抛物线C1关于原点对称的抛物线C2的解析式;
(2)设抛物线C1的顶点为M,抛物线C2与x轴分别交于C,D两点(点C在点D的左侧),顶点为N,四边形MDNA的面积为S,若点A,点D同时以每秒1个单位的速度沿水平方向分别向右、向左运动;与此同时,点M,点N同时以每秒2个单位的速度沿坚直方向分别向下、向上运动,直到点A与点D重合为止,求出四边形MDNA的面积S与运动时间t之间的关系式,并写出自变量t的取值范围;
(3)当t为何值时,四边形MDNA的面积S有最大值,并求出此最大值;
(4)在运动过程中,四边形MDNA能否形成矩形?若能,求出此时t的值;若不能,请说明理由。
(1)求抛物线C1关于原点对称的抛物线C2的解析式;
(2)设抛物线C1的顶点为M,抛物线C2与x轴分别交于C,D两点(点C在点D的左侧),顶点为N,四边形MDNA的面积为S,若点A,点D同时以每秒1个单位的速度沿水平方向分别向右、向左运动;与此同时,点M,点N同时以每秒2个单位的速度沿坚直方向分别向下、向上运动,直到点A与点D重合为止,求出四边形MDNA的面积S与运动时间t之间的关系式,并写出自变量t的取值范围;
(3)当t为何值时,四边形MDNA的面积S有最大值,并求出此最大值;
(4)在运动过程中,四边形MDNA能否形成矩形?若能,求出此时t的值;若不能,请说明理由。

|
解:(1)点A(-4,0),点B(-2,0),点E(0,8)关于原点的对称点分别为D(4,0),C(2,0),F(0,-8), |
 |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ,
,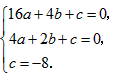
 ,
, ;
; ,垂足为H,
,垂足为H, ,
, ,所以四边形MDNA是平行四边形,
,所以四边形MDNA是平行四边形, ,
, ,
,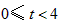 ,所以,所求关系式是
,所以,所求关系式是 ,t的取值范围是
,t的取值范围是 ;
;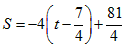 ,(
,( ),
), 时,S有最大值
时,S有最大值 ,
, ,
, ,
, ,
, (舍),
(舍), 。
。 
 的左侧),点B的横坐标是1;
的左侧),点B的横坐标是1;