Question

如图，边长为2的正方形ABCD放在平面直角坐标系中，将正方形绕点B顺时针旋转45°，得到正方形A′BC′D′，此时C′的坐标为______．

Answer 1

作C′E⊥x轴于E点，如图，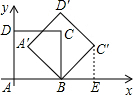
∵将边长为2的正方形绕点B顺时针旋转45°，得到正方形A′BC′D′，
∴AB=BC′=BC=2，∠CBC′=45°，
∴∠EBC′=45°，
∴△BEC′为等腰直角三角形，
∴BE=C′E=

2

2

BC′=

2

，
∴AE=AB+BE=2+

2

，
∴C′点坐标为（2+

2

，

2

）．
故答案为（2+

2

，

2

）．