Question

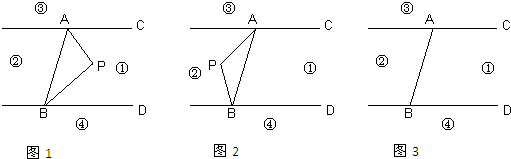
如图，直线AC∥BD，连结AB，直线AC、BD及线段AB把平面分成①、②、③、④四个部分，规定：线上各点不属于任何部分．当动点P落在某个部分时，连结PA、PB，构成∠PAC、∠APB、∠PBD三个角． (提示：有公共端点的两条重合的射线所组成的角是0°)

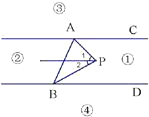
1.当动点P落在第①部分时，有∠APB＝∠PAC＋∠PBD，请说明理由；

2.当动点P落在第②部分时，∠APB＝∠PAC＋∠PBD是否成立（直接回答成立或不成立）？

3.当动点P在第③部分时，探究∠PAC、∠APB、∠PBD之间的关系，直接写出你发现的结论．

 

Answer 1

 

1.过点P作直线AC的平行线（如图），易知∠1=∠PAC，∠2=∠PBD，

又∵∠APB=∠1+∠2，

∴∠APB=∠PAC+∠PBD．

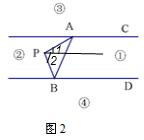
2.不成立．

过点P作AC的平行线PQ，∠APB=∠1+∠2，

∵直线AC∥BD，

∴∠PAC+∠1=180°，∠PBD+∠2=180°，

∴∠PAC+∠1+∠PBD+∠2=360°，

故∠APB=∠PAC+∠PBD不成立．（

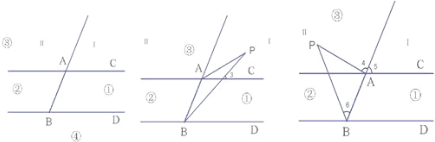
3.设射线BA将区域③分成Ⅰ、Ⅱ两部分（如左图），

①若点P位于第Ⅰ部分（如中图），则∠PBD=∠3，∠PAC+∠APB=∠3，

所以∠APB=∠PBD-∠PAC，

②若点P位于第Ⅱ部分（如右图），则∠PBD=∠6+∠ABD，∠PAC=∠4+∠5，∠ABD=∠5，

∴∠PAC-∠PBD=∠4-∠6，

而∠6+∠APB=∠4，

∴∠APB=∠PAC-∠PBD．

③P落在射线BA上时，∠PAC=∠PBD，∠APB=0°．

解析:

1.过点P作AC的平行线，根据平行线的性质将∠PAC，∠PBD等量转化，证出结论．

2.过点P作AC的平行线PQ，∠APB=∠APQ+∠QPB，∠PAC与∠APQ是一对同旁内角，∠QPB与∠PBD也是一对同旁内角，根据两直线平行，同旁内角互补，发现三个角的和是360度．

3.根据BA的延长线上，或两侧分别解答．