题目内容
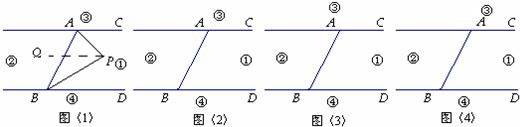
如图,直线AC∥BD,连接AB,直线AC,BD及线段AB把平面分成①、②、③、④四个部分,规定:线上各点不属于任何部分.当动点P落在某个部分时,连接PA,PB,构成∠PAC,∠APB,∠PBD三个角.(提示:有公共端点的两条重合的射线所组成的角是0°角)
(1)当动点P落在第①部分时,试说明∠APB=∠PAC+∠PBD;
(2)当动点P落在第②部分时,∠APB=∠PAC+∠PBD是否成立?(直接回答成立或不成立)
(3)当动点P在第③部分时,全面探究∠PAC,∠APB,∠PBD之间的关系,并写出动点P的具体位置和相应的结论.选择其中一种结论加以说明.

(1)当动点P落在第①部分时,试说明∠APB=∠PAC+∠PBD;
(2)当动点P落在第②部分时,∠APB=∠PAC+∠PBD是否成立?(直接回答成立或不成立)
(3)当动点P在第③部分时,全面探究∠PAC,∠APB,∠PBD之间的关系,并写出动点P的具体位置和相应的结论.选择其中一种结论加以说明.

分析:(1)延长AP交BD于M,根据三角形外角性质和平行线性质得出∠APB=∠AMB+∠PBD,∠PAC=∠AMB,代入求出即可;
(2)过P作EF∥AC,根据平行线性质得出∠PAC+∠APF=180°,∠PBD+∠BPF=180°,即可得出答案;
(3))①当动点P在射线BA的右侧时,结论是∠PBD=∠PAC+∠APB,②当动点P在射线BA上时,结论是:∠PBD=∠PAC+∠APB(或∠PAC=∠PBD+∠APB或∠APB=0°),③当动点P在射线BA的左侧时,结论是:∠PAC=∠APB+∠PBD,根据三角形外角性质和平行线性质求出即可.
(2)过P作EF∥AC,根据平行线性质得出∠PAC+∠APF=180°,∠PBD+∠BPF=180°,即可得出答案;
(3))①当动点P在射线BA的右侧时,结论是∠PBD=∠PAC+∠APB,②当动点P在射线BA上时,结论是:∠PBD=∠PAC+∠APB(或∠PAC=∠PBD+∠APB或∠APB=0°),③当动点P在射线BA的左侧时,结论是:∠PAC=∠APB+∠PBD,根据三角形外角性质和平行线性质求出即可.
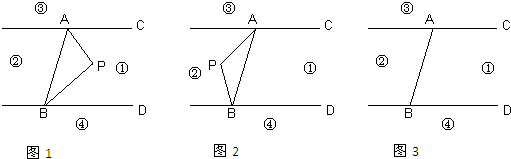
解答:解:(1)延长AP交BD于M,如图1,

∵AC∥BD,
∴∠PAC=∠AMB,
∵∠APB=∠AMB+∠PBD,
∴∠APB=∠PAC+∠PBD.
(2)∠APB=∠PAC+∠PBD不成立,如图2,

理由是:过P作EF∥AC,
∵AC∥BD,
∴AC∥EF∥BD,
∴∠PAC+∠APF=180°,∠PBD+∠BPF=180°,
∴∠PAC+∠APF+∠PBD+∠BPF=360°,
∴∠APB+∠PAC+∠PBD=360°,
∴∠APB=360°-∠PAC-∠PBD,
∵∠APB≠180°,
∴∠APB=∠PAC+∠PBD不成立.
(3)①当动点P在射线BA的右侧时,如图3,结论是∠PBD=∠PAC+∠APB,

理由是:∵AC∥BD,
∴∠PMC=∠PBD,
∵∠PMC=∠PAC+∠APB,
∴∠PBD=∠PAC+∠APB.
②当动点P在射线BA上时,如图4,结论是:∠PBD=∠PAC+∠APB(或∠PAC=∠PBD+∠APB或∠APB=0°),

理由是:∵AC∥BD,
∴∠PAC=∠PBD,
∵∠APB=0°,
∴∠PBD=∠PAC+∠APB或∠PAC=∠PBD+∠APB.
③当动点P在射线BA的左侧时,如图5,结论是:∠PAC=∠APB+∠PBD,

理由是:∵AC∥BD,
∴∠PMC=∠PBD,
∵∠PAC=∠APB+∠PMC,
∴∠PAC=∠APB+∠PBD.

∵AC∥BD,
∴∠PAC=∠AMB,
∵∠APB=∠AMB+∠PBD,
∴∠APB=∠PAC+∠PBD.
(2)∠APB=∠PAC+∠PBD不成立,如图2,

理由是:过P作EF∥AC,
∵AC∥BD,
∴AC∥EF∥BD,
∴∠PAC+∠APF=180°,∠PBD+∠BPF=180°,
∴∠PAC+∠APF+∠PBD+∠BPF=360°,
∴∠APB+∠PAC+∠PBD=360°,
∴∠APB=360°-∠PAC-∠PBD,
∵∠APB≠180°,
∴∠APB=∠PAC+∠PBD不成立.
(3)①当动点P在射线BA的右侧时,如图3,结论是∠PBD=∠PAC+∠APB,

理由是:∵AC∥BD,
∴∠PMC=∠PBD,
∵∠PMC=∠PAC+∠APB,
∴∠PBD=∠PAC+∠APB.
②当动点P在射线BA上时,如图4,结论是:∠PBD=∠PAC+∠APB(或∠PAC=∠PBD+∠APB或∠APB=0°),

理由是:∵AC∥BD,
∴∠PAC=∠PBD,
∵∠APB=0°,
∴∠PBD=∠PAC+∠APB或∠PAC=∠PBD+∠APB.
③当动点P在射线BA的左侧时,如图5,结论是:∠PAC=∠APB+∠PBD,

理由是:∵AC∥BD,
∴∠PMC=∠PBD,
∵∠PAC=∠APB+∠PMC,
∴∠PAC=∠APB+∠PBD.
点评:本题考查了平行线的性质和三角形外角性质的应用,用了分类讨论思想.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2012•桂平市三模)如图,直线AC∥BD,⊙O与AC和BD分别相切于点A和点B.点M和点N分别是AC和BD上的动点,MN沿AC和BD平移.⊙O的半径为1,∠1=60°.下列结论错误的是( )
(2012•桂平市三模)如图,直线AC∥BD,⊙O与AC和BD分别相切于点A和点B.点M和点N分别是AC和BD上的动点,MN沿AC和BD平移.⊙O的半径为1,∠1=60°.下列结论错误的是( )