题目内容
【题目】如图所示已知![]() ,
,![]() ,OM平分
,OM平分![]() ,ON平分
,ON平分![]() ;
;
(1)![]() ;
;
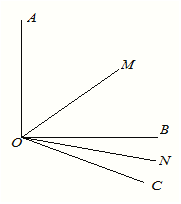
(2)如图∠AOB=900,将OC绕O点向下旋转,使∠BOC=![]() ,仍然分别作∠AOC,∠BOC的平分线OM,ON,能否求出∠MON的度数,若能,求出其值,若不能,试说明理由.
,仍然分别作∠AOC,∠BOC的平分线OM,ON,能否求出∠MON的度数,若能,求出其值,若不能,试说明理由.

(3)![]() ,
,![]() ,仍然分别作∠AOC,∠BOC的平分线OM,ON,能否求出∠MON的度数,若能,求
,仍然分别作∠AOC,∠BOC的平分线OM,ON,能否求出∠MON的度数,若能,求![]() 的度数;并从你的求解中看出什么什么规律吗?
的度数;并从你的求解中看出什么什么规律吗?

【答案】(1)![]() ;
;
(2)能,因为∠AOB=900,∠BOC=![]() , 所以∠AOC=900+
, 所以∠AOC=900+![]() ,
,
因为OM、 ON平分∠AOC,∠BOC的线
所以∠MOC=![]() ∠AOC=
∠AOC=![]() (900+
(900+![]() )=450+x
)=450+x
所以∠CON=![]() ∠BOC=x
∠BOC=x
所以∠MON=∠MOC-∠CON=450+x-x=450
(3)能,因为∠AOB=![]() ,∠BOC=
,∠BOC=![]() ,
,
所以∠AOC=![]() +
+![]() ,
,
因为OM、 ON平分∠AOC,∠BOC的线
所以∠MOC=![]() ∠AOC=
∠AOC=![]() (
(![]() +
+![]() )
)
所以∠CON=![]() ∠BOC=
∠BOC=![]()
![]()
所以∠MON=∠MOC-∠CON=![]() (
(![]() +
+![]() )-
)-![]()
![]() =
=![]()
![]()
即![]() .
.
【解析】
(1)根据题意可知,∠AOC=120°,由OM平分∠AOC,ON平分∠BOC;推出∠MOC=∠AOC=60°,∠CON=![]() ∠BOC=15°,由图形可知,∠MON=∠MOC-∠CON,即∠MON=45°;(2)根据(1)的求解思路,先利用角平分线的定义表示出∠MOC与∠NOC的度数,然后相减即可得到∠MON的度数;(3)用α、β表示∠MOC,∠NOC,根据∠MON=∠MOC-∠NOC得到.
∠BOC=15°,由图形可知,∠MON=∠MOC-∠CON,即∠MON=45°;(2)根据(1)的求解思路,先利用角平分线的定义表示出∠MOC与∠NOC的度数,然后相减即可得到∠MON的度数;(3)用α、β表示∠MOC,∠NOC,根据∠MON=∠MOC-∠NOC得到.
(1)(1)∵∠AOB=90°,∠BOC=30°,
∴∠AOC=∠AOB+∠BOC=90°+30°=120°,
∵OM平分∠AOC,ON平分∠BOC,
∴∠MOC=∠AOC=60°,∠CON=![]() ∠BOC=15°,
∠BOC=15°,
∴∠MON=∠MOC-∠CON=60°-15°=45°;
故答案为:45;
(2)能.∵∠AOB=90°,∠BOC=2x°,
∴∠AOC=90°+2x°,
∵OM、ON分别平分∠AOC,∠BOC,
∴∠MOC=![]() ∠AOC=
∠AOC=![]() (90°+2x°)=45°+x,
(90°+2x°)=45°+x,
∴∠CON=![]() ∠BOC=x,
∠BOC=x,
∴∠MON=∠MOC-∠CON=45°+x-x=45°
(3))∵∠AOB=α,∠BOC=β,
∴∠AOC=∠AOB+∠BOC=α+β,
∵OM平分∠AOC,
∴∠MOC=![]() ∠AOC=
∠AOC=![]() (α+β),
(α+β),
∵ON平分∠BOC,
∴∠NOC=![]() ∠BOC=
∠BOC=![]() ,
,
∴∠MON=∠MOC-∠NOC=![]() (α+β)-
(α+β)-![]() =
=![]() .
.

 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案



