题目内容
【题目】如图,在矩形ABCD中,点E在AD上,EC平分∠BED.
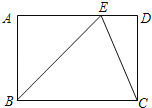
(1)△BEC是否为等腰三角形?为什么?
(2)若AB=a,∠ABE=45°,求BC的长.
【答案】(1)是等腰三角形,理由见解析(2)![]() a
a
【解析】
试题分析:(1)求出∠DEC=∠ECB=∠BEC,推出BE=BC即可;
(2)求出AE=AB=a,根据勾股定理求出BE即可.
解:(1)△BEC是等腰三角形,理由如下:
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠DEC=∠BCE,
∵EC平分∠DEB,
∴∠DEC=∠BEC,
∴∠BEC=∠ECB,
∴BE=BC,
即△BEC是等腰三角形.
(2)∵四边形ABCD是矩形,
∴∠A=90°,
∵∠ABE=45°,
∴∠ABE=AEB=45°,
∴AB=AE=a,
由勾股定理得:BE=![]() =
=![]() a,
a,
即BC=BE=![]() a.
a.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目