Question

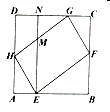
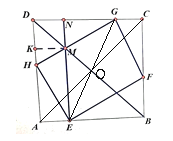
【题目】如图，平行四边形的四个顶点分别在正方形的四条边上.，分别交，，于点，，，且.要求得平行四边形的面积，只需知道一条线段的长度.这条线段可以是（ ）

A.B.C.D.

Answer 1

【答案】C

【解析】

根据图形证明△AOE≌△COG，作KM⊥AD，证明四边形DKMN为正方形，再证明Rt△AEH≌Rt△CGF，Rt△DHG≌Rt△BFE，设正方形边长为a，CG=MN=x，根据正方形的性质列出平行四边形的面积的代数式，再化简整理，即可判断.

连接AC,EG，交于O点，

∵四边形是平行四边形，四边形是正方形，

∴GO=EO,AO=CO,

又∠AOE=∠COG

∴△AOE≌△COG，

∴GC=AE,

∵NE∥AD，

∴四边形AEND为矩形，

∴AE=DN,

∴DN=GC=MN

作KM⊥AD，

∴四边形DKMN为正方形，

在Rt△AEH和Rt△CGF中，

∴Rt△AEH≌Rt△CGF，

∴AH=CF,

∵AD-AH=BC-CF

∴DH=BF,

同理Rt△DHG≌Rt△BFE，

设CG=MN=x，

设正方形边长为a

则S△HDG=DH×x+DG×x=S△FBE

S△HAE=AH×x =S△GCF

S平行四边形EFGH=a2-2S△HDG-2S△HAE= a2-(DH+DG+AH)×x,

∵DG=a-x

∴S平行四边形EFGH= a2-(a+a-x)×x= a2-2ax+x2= (a-x)2

故只需要知道a-x就可以求出面积

BE=a-x，故选C.