题目内容
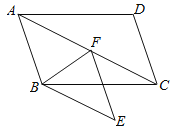
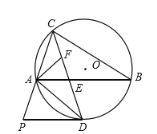
【题目】如图,圆![]() 是锐角
是锐角![]() 的外接圆,
的外接圆,![]() 是弧
是弧![]() 的中点,
的中点,![]() 交
交![]() 于点
于点![]() ,
,![]() 的平分线交
的平分线交![]() 于点
于点![]() ,过点
,过点![]() 的切线交
的切线交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() ,则有下列结论:①点
,则有下列结论:①点![]() 是
是![]() 的重心;②
的重心;②![]() ;③
;③![]() ;④
;④![]() ,其中正确结论的序号是__________.
,其中正确结论的序号是__________.
【答案】②④
【解析】
根据三角形重心的定义,即可判断①;连接OD,根据垂径定理和切线的性质定理,即可判断②;由∠ACD=∠BAD,∠CAF=∠BAF,得∠AFD=∠FAD,若![]() ,可得∠EAF=∠ADF=
,可得∠EAF=∠ADF=![]() ∠BAC,进而得
∠BAC,进而得![]() ,即可判断③;易证ACD~EAD,从而得
,即可判断③;易证ACD~EAD,从而得![]() ,结合DF=DA,即可判断④.
,结合DF=DA,即可判断④.
∵![]() 是弧
是弧![]() 的中点,
的中点,
∴∠ACD=∠BCD,即:CD是∠ACB的平分线,
又∵AF是![]() 的平分线,
的平分线,
∴点F不是![]() 的重心,
的重心,
∴①不符合题意,
连接OD,
∵![]() 是弧
是弧![]() 的中点,
的中点,
∴OD⊥AB,
∵PD与圆![]() 相切,
相切,
∴OD⊥PD,
∴![]() ,
,
∴②符合题意,
∵![]() 是弧
是弧![]() 的中点,
的中点,
∴∠ACD=∠BAD,
∵AF是![]() 的平分线,
的平分线,
∴∠CAF=∠BAF,
∴∠CAF+∠ACD =∠BAF+∠BAD,即:∠AFD=∠FAD,
若![]() ,则∠AFD=∠AEF,
,则∠AFD=∠AEF,
∴∠AFD=∠AEF=∠FAD,
∴∠EAF=∠ADF=![]() ∠BAC,
∠BAC,
∴![]() .
.
即:只有当![]() 时,才有
时,才有![]() .
.
∴③不符合题意,
∵∠ACD=∠BAD,∠D=∠D,
∴ACD~EAD,
∴![]() ,
,
又∵∠AFD=∠FAD,
∴DF=DA,
∴![]() ,
,
∴④符合题意.
故答案是:②④.


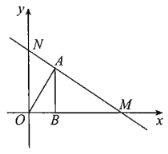
【题目】如图,点M的坐标为![]() ,点A在第一象限,
,点A在第一象限,![]() 轴,垂足为B,
轴,垂足为B,![]() .
.
(1)如果![]() 是等腰三角形,求点A的坐标;
是等腰三角形,求点A的坐标;
(2)设直线MA与y轴交于点N,则是否存在![]() 与
与![]() 相似?若存在,请直接写出点A的坐标;若不存在,请说明理由.
相似?若存在,请直接写出点A的坐标;若不存在,请说明理由.
【题目】某商场经市场调查,发现进价为40元的台灯每月的销售量y(台)与售价x(元)的相关信息如下:
售价x(元) | 50 | 60 | 70 | 80 | …… |
销售量y(台) | 200 | 180 | 160 | 140 | …… |
(1)试用你学过的函数来描述y与x的关系,这个函数可以是 函数,求这个函数关系式;
(2)售价为多少元时,当月的利润最大?最大利润是多少?