题目内容
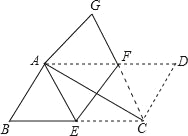
【题目】如图，将ABCD沿EF折叠，恰好使点C与点A重合，点D落在点G处，连接AC、CF．
（1）求证：△ABE≌△AGF．
（2）判断四边形AECF的形状，说明理由．
【答案】（1）详见解析；（2）边形AECF是菱形，理由详见解析.
【解析】分析：（1）由四边形ABCD是平行四边形与折叠性质，易得AB=AG，∠BAE=∠GAF，∠BEA=∠EAF=∠GFA，则可利用AAS判定：△ABE≌△AGF．
（2）由（1）易证得EC=AE=AF，又由AF∥EC，即可判定四边形AECF是菱形．
详解：（1）∵四边形ABCD是平行四边形，∴AB=CD，∠BAD=∠BCD，由折叠的性质得：AG=CD，∠EAG=∠BCD，∴AB=AG，∠BAD=∠EAG，∴∠BAE=∠GAF．
又∵AB∥CD，AE∥GF，AD∥BC，∴∠BEA=∠EAF=∠GFA．在△ABE和△AGF中，∵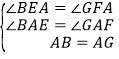
，∴△ABE≌△AGF（AAS）；
（2）四边形AECF是菱形．理由如下：
由折叠的性质得：EC=AE．
∵△ABE≌△AGF，∴AE=AF，∴EC=AE=AF．
∵AF∥EC，∴四边形AECF是平行四边形，∴AECF是菱形．
练习册系列答案
心算口算巧算一课一练系列答案
相关题目
