题目内容
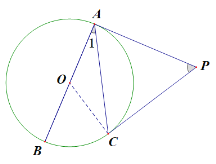
【题目】如图a,AB为⊙O直径,AC为⊙O的为弦,PA为⊙O的切线,∠APC=2∠1.
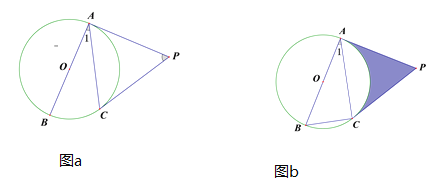
(1)求证:PC是⊙O的切线.
(2)当∠1=30°,AB=4时,其他条件不变,求图b中阴影部分的面积.
【答案】(1)见解析;(2)4![]() -
-![]() π
π
【解析】
(1)连接OC,首先证明∠APC+∠AOC=180°,由PA是圆的切线可得∠OAP=90°,根据四边形内角和可得∠OCP=90°,从而得证;
(2)
(1)证明:连结OC.
在圆O中,OA=OC,
∴∠BOC=2∠1=∠APC
∠BOC+∠AOC=180°
∴∠APC+∠AOC=180°
∵PA为⊙O的切线,
∴∠OAP=90°
又四边形内角和为360°,
∴∠OCP=90°,OC为⊙O的半径
∴PC为⊙O的切线.
(2)∵PA为⊙O的切线,PC为⊙O的切线.
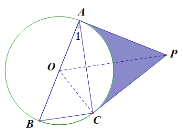
∴PA=PC
∵∠1=30°,∠APC=2∠1
∴∠APC=60°,∠AOC=120°,
∴△APC为等边三角形.
连结OP,OC,则∠APO=∠CPO=30°
∵AB=4
∴OC=OA=2,
在Rt△POA中,PO=4,PA=2![]() ,
,
∴S四边形AOCP=2×![]() ×2×2
×2×2![]() =4
=4![]() ,
,
S扇形AOC=![]() ×π×4=
×π×4=![]() π
π
S阴影部分的面积=4![]() -
-![]() π.
π.

 期末冲刺100分创新金卷完全试卷系列答案
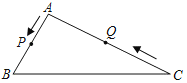
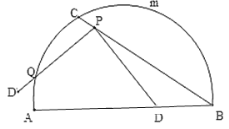
期末冲刺100分创新金卷完全试卷系列答案【题目】如图,C是![]() 的一定点,D是弦AB上的一定点,P是弦CB上的一动点.连接DP,将线段PD绕点P顺时针旋转
的一定点,D是弦AB上的一定点,P是弦CB上的一动点.连接DP,将线段PD绕点P顺时针旋转![]() 得到线段
得到线段![]() .射线
.射线![]() 与
与![]() 交于点Q.已知
交于点Q.已知![]() ,设P,C两点间的距离为xcm,P,D两点间的距离
,设P,C两点间的距离为xcm,P,D两点间的距离![]() ,P,Q两点的距离为
,P,Q两点的距离为![]() .
.
小石根据学习函数的经验,分别对函数![]() ,
,![]() ,随自变量x的变化而变化的规律进行了探究,下面是小石的探究过程,请补充完整:
,随自变量x的变化而变化的规律进行了探究,下面是小石的探究过程,请补充完整:
(1)按照下表中自变量x的值进行取点、画图、测量,分别得到了![]() ,
,![]() ,与x的几组对应值:
,与x的几组对应值:
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 4.29 | 3.33 | 1.65 | 1.22 | 1.50 | 2.24 | |
| 0.88 | 2.84 | 3.57 | 4.04 | 4.17 | 3.20 | 0.98 |
(2)在同一平面直角坐标系xOy中,描出补全后的表中各组数据所对应的点![]() ,
,![]() ,并画出函数
,并画出函数![]() ,
,![]() 的图象;
的图象;
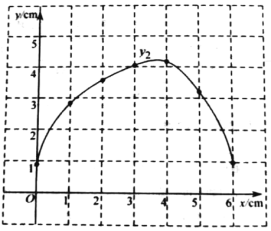
(3)结合函数图象,解决问题:连接DQ,当△DPQ为等腰三角形时,PC的长度约为_____cm.(结果保留一位小数)