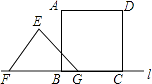Question

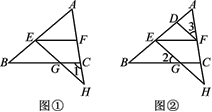
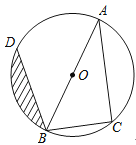
【题目】如图，在矩形ABCD中，O为AC中点，EF过点O且EF⊥AC分别交DC于点F，交AB于点E，点G是AE中点且∠AOG=30°，给出以下结论： ①∠AFC=120°；
②△AEF是等边三角形；
③AC=3OG；
④S△AOG= S△ABC
其中正确的是 ． （把所有正确结论的序号都选上）

Answer 1

【答案】①②④
【解析】解：∵四边形ABCD是矩形， ∴AB∥CD，∠B=90°，
∴∠FCA=∠OAG，
∵O为AC中点，EF⊥AC，
∴AF=CF，
∴∠FAC=∠FCA，
∵点G是AE中点且∠AOG=30°，
∴OG= AE=AG，
∴∠OAG=∠AOG=30°，
∴∠FCA=∠FAC=30°，
∴∠AFC=180°﹣30°﹣30°=120°，①正确；
∵∠FAE=30°+30°=60°，∠AEO=90°﹣30°=60°，
∴∠AFE=60°，
∴△AEF是等边三角形，②正确；
∵∠OAG=30°，EF⊥AC，
∴AE=2OE=2OG，
∴OA= OE= OG，
∴AC=2OA=2 OG，③不正确；
∵点G是AE中点，
∴S△AOG= S△AOE ，
∵∠AOE=90°=∠B，∠OAE=∠BAC，
∴△AOE∽△ABC，相似比为 = = = ，
∴ =（ ）= ，
∴S△AOG= S△ABC ， ④正确；
故答案为：①②④．
由矩形的性质得出AB∥CD，∠B=90°，得出∠FCA=∠OAG，由线段垂直平分线的性质得出AF=CF，得出∠FAC=∠FCA，由直角三角形的性质得出OG= AE=AG，得出∠OAG=∠AOG=30°，求出∠FCA=∠FAC=30°，再由三角形内角和定理得出①正确；求出∠FAE=∠AEO=∠AFE=60°，得出△AEF是等边三角形，②正确；由含30°角的直角三角形的性质和勾股定理得出OA= OE= OG，得出AC=2OA=2 OG，③不正确；由中点的性质得出S△AOG= S△AOE ， 证明△AOE∽△ABC，得出 = ，得出S△AOG= S△ABC ， ④正确，即可得出结论．