题目内容
【题目】在平面直角坐标中,A (0,5)、B (4,0)、C (2,5),四边形AOBC经过平移后得到四边形A′O′B′C′.

(1) 如图1,若A′(-3,5),四边形AOBC内部一点M(a+b-2,6a-7)经过平移后得到点N(a+2b-7,4b-6),求M点的坐标
(2) 如图2,若四边形AOBC向右平移m个单位长度(m>0).当m为何值时,重叠部分的面积比四边形BB′C′C的面积大
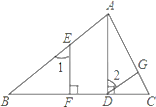
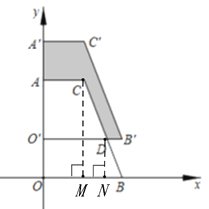
(3) 如图3,若四边形AOBC向上平移2个单位长度,直接写出图中阴影部分的面积.
【答案】(1)![]() ;(2)当
;(2)当![]() 时,重叠部分的面积比四边形BB′C′C的面积大;(3)
时,重叠部分的面积比四边形BB′C′C的面积大;(3)![]()
【解析】
(1)根据对应点的横坐标和纵坐标的变化确定平移方向和平移距离;
(2)用m表示线段长,根据梯形面积公式表示出重叠部分和四边形BB′C′C的面积,根据二者的关系列出不等式求解;
(3)根据平移性质和勾股定理求出OD的长度,由图形特征得出阴影部分的面积等于梯形OBDO的面积,根据梯形面积公式计算.
(1)∵A (0,5),A′(-3,5),
∴四边形AOBC向左平移3个单位得到四边形A′O′B′C′,
∵M(a+b-2,6a-7)对应点为N(a+2b-7,4b-6),
∴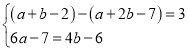 ,
,
∴![]() ,
,
∴M点的坐标为:![]() .
.
(2)∵A (0,5)、B (4,0)、C (2,5),
∴AO=5,AC=2,OB=4,
根据题意得,![]() ,
,
解得,![]() ,
,
∴![]() .
.
∴当![]() 时,重叠部分的面积比四边形BB′C′C的面积大.
时,重叠部分的面积比四边形BB′C′C的面积大.
(3)如图,由图形可得,阴影部分的面积等于梯形OBDO的面积,
过C作CM⊥x轴于M点,作DN⊥x轴于N点,
∴∠OND=∠NDO=∠OON=90°,
∴四边形ONDO是矩形,∴ON=OD,OO=ND=2
∵∠AOM=∠OMC=∠OAC=90°,
∴四边形OMCA是矩形,
∴CM=OA=5,AC=OM=2
∴BM=OB-OM=4-2=2,
在Rt△CMB中,由勾股定理得BC=![]() ,
,
∵AC∥OD∥OB,
∴![]() ,
,
∴![]() ,
,
∴BD=![]() ,
,
在Rt△DNB中,由勾股定理得,BN=![]() ,
,
∴ON=OB-BN=4-![]() =
=![]() ,
,
∴ON=OD=![]() ,
,
∴S梯形OBDO=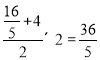 .
.
即阴影部分的面积为![]() .
.

 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案【题目】某学校随机选取40名学生进行军运会知识考查,对考查成绩进行统计(成绩均为整数),并依据统计数据绘制了如下统计图表.解答下列问题:
组别 | 分数段/分 | 频数 | 频率 |
1 | 50.5~60.5 | 2 | a |
2 | 60.5~70.5 | 6 | 0.15 |
3 | 70.5~80.5 | b | c |
4 | 80.5~90.5 | 12 | 0.30 |
5 | 90.5~100.5 | 6 | 0.15 |
合计 | 40 | 1.00 | |

(1) 表中a=______;b=______;c=____;
(2) 请补全频数分布直方图;
(3) 已知该学校共有学生1280人,若考查成绩80分以上(不含80分)为优秀,试估计该学校学生军运会知识考查成绩达到优秀的人数.