题目内容
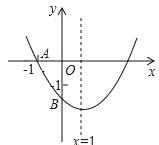
【题目】已知函数 y =kx2 +(k +1)x +1(k 为实数),
(1)当 k=3 时,求此函数图象与 x 轴的交点坐标;
(2)判断此函数与 x 轴的交点个数,并说明理由;
(3)当此函数图象为抛物线,且顶点在 x 轴下方,顶点到 y 轴的距离为 2,求 k 的值.
【答案】(1)函数图象与 x 轴的交点坐标为(-1,0),(- ![]() ,0);
,0);
(2)当 k=0 或 1 时, 它的图象与 x 轴有一个公共点; 当 k≠0 且 k≠1 时,图象与与 x 轴有两个公共点;(3)顶点坐标为(-2,-![]() ).
).
【解析】试题分析: ![]() 令
令![]() 即可求出此函数与
即可求出此函数与![]() 轴的交点坐标.
轴的交点坐标.
![]() 分
分![]() 和
和![]() 两种情况进行讨论.
两种情况进行讨论.
![]() 顶点到
顶点到![]() 轴的距离为 2,即
轴的距离为 2,即![]() 即可求得
即可求得![]() 的值.
的值.
试题解析:(1)![]()
![]()
令 ![]()
![]()
解得: ![]()
∴此函数图象与 x 轴的交点坐标为![]()
![]()
①当![]() 时,
时,
函数为 ![]()
此函数图象与 x 轴有一个公共点;
②当![]() 时,
时,
![]()
若 ![]() 则
则![]() ,它的图象与 x轴有一个公共点;
,它的图象与 x轴有一个公共点;
若![]() 则
则![]() ,它的图象与x 轴有两个公共点;
,它的图象与x 轴有两个公共点;
当 ![]() 或 1 时, 它的图象与 x轴有一个公共点;
或 1 时, 它的图象与 x轴有一个公共点;
当 ![]() 且
且 ![]() 时,图象与与x 轴有两个公共点.
时,图象与与x 轴有两个公共点.
(3)依题可得:
![]() 解得
解得![]() 或
或![]()
①当![]() 时,
时,
![]()
顶点坐标为![]()
顶点在 x 轴下方,满足题意;
②当![]() 时,
时,
![]()
∴顶点坐标为![]()
∴顶点在 x 轴上方,不符合题意.

练习册系列答案
相关题目