题目内容
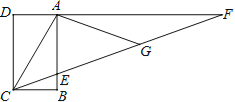
【题目】完成下列证明:如图,已知AD⊥BC,EF⊥BC,∠1=∠2.
求证: DG∥BA.
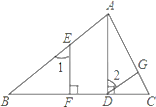
证明:∵AD⊥BC,EF⊥BC ( 已知 )
∴∠EFB=90°,∠ADB=90°(_______________________ )
∴∠EFB=∠ADB ( 等量代换 )
∴EF∥AD ( _________________________________ )
∴∠1=∠BAD (________________________________________)
又∵∠1=∠2 ( 已知)
∴ (等量代换)
∴DG∥BA. (__________________________________)
【答案】垂直的定义;同位角相等,两直线平行;两直线平行,同位角相等;∠BAD=∠2,内错角相等,两直线平行.
【解析】
先由垂直的定义得出两个90°的同位角,根据同位角相等判定两直线平行,根据两直线平行,同位角相等得到∠1=∠BAD,再根据等量代换得出∠BAD=∠2,最后根据内错角相等,两直线平行即可判定.
证明:∵AD⊥BC,EF⊥BC ( 已知 )
∴∠EFB=90°,∠ADB=90°( 垂直的定义 )
∴∠EFB=∠ADB ( 等量代换 )
∴EF∥AD ( 同位角相等,两直线平行 )
∴∠1=∠BAD ( 两直线平行,同位角相等 )
又∵∠1=∠2 ( 已知)
∴ ∠BAD=∠2 (等量代换)
∴DG∥BA. ( 内错角相等,两直线平行 )

练习册系列答案
相关题目