题目内容
【题目】如图,等边三角形ABD和等边三角形CBD的边长均为a,现把它们拼合起来,E是AD上异于A、D两点的一动点,F是CD上一动点,满足AE+CF=a.则△BEF的形状如何?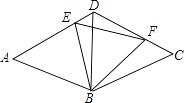
【答案】解:△BEF为正三角形证明:∵AE+CF=a,AE+ED=a,
∴DE=CF,
在△BDE和△BCF中, ,
,
∴△BDE≌△BCF,
∴BE=BF,∠CBF=∠DBE,
又∵∠CBF+∠FBD=60°,
∴∠FBD+∠DBE=60°,
∴△BEF为等边三角形
【解析】结论:△BEF为正三角形。理由:要证一个三角形为正三角形,可根据有一个角等于![]() 的等腰三角形是等边三角形来判断。首先可根据已知条件用边角边证明△BDE≌△BCF,得出BE=BF,∠CBF=∠DBE,而∠CBF+∠FBD=60°,所以可得∠FBD+∠DBE=60°,即∠EBF=60°,结论可证。
的等腰三角形是等边三角形来判断。首先可根据已知条件用边角边证明△BDE≌△BCF,得出BE=BF,∠CBF=∠DBE,而∠CBF+∠FBD=60°,所以可得∠FBD+∠DBE=60°,即∠EBF=60°,结论可证。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目