题目内容
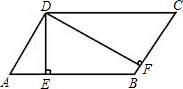
如图所示．?ABCD中，DE⊥AB于E，BM=MC=DC．求证：∠EMC=3∠BEM．
证明：延长EM交DC的延长线于F，连接DM．
∵CM=BM，∠F=∠BEM，∠MCF=∠B，
∴△MCF≌△MBE（AAS），
∴M是EF的中点．由于AB∥CD及DE⊥AB，
∴DE⊥FD，三角形DEF是直角三角形，DM为斜边的中线，
由直角三角形斜边中线的性质知∠F=∠MDC，又由已知MC=CD，
∴∠MDC=∠CMD，
则∠MCF=∠MDC+∠CMD=2∠F．
从而∠EMC=∠F+∠MCF=3∠F=3∠BEM．
∵CM=BM，∠F=∠BEM，∠MCF=∠B，
∴△MCF≌△MBE（AAS），
∴M是EF的中点．由于AB∥CD及DE⊥AB，
∴DE⊥FD，三角形DEF是直角三角形，DM为斜边的中线，
由直角三角形斜边中线的性质知∠F=∠MDC，又由已知MC=CD，
∴∠MDC=∠CMD，
则∠MCF=∠MDC+∠CMD=2∠F．
从而∠EMC=∠F+∠MCF=3∠F=3∠BEM．
练习册系列答案
相关题目
学公式或定理吗？相信你能给出简明的推理过程．
