题目内容
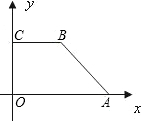
在直角梯形OABC中,OA∥BC,A、B两点的坐标分别为A(13,0),B(11,12),动点P、Q同时从O、B两点出发,点P以每秒2个单位的速度沿OA向终点A运动,点Q以每秒1个单位的速度沿BC向C运动,当点P停止运动时,点Q同时停止运动.线段OB、PQ相交于点D,过点D作DE∥OA,交AB于点E,射线QE交 轴于点F(如图).设动点P、Q运动时间为t(单位:秒),则:
轴于点F(如图).设动点P、Q运动时间为t(单位:秒),则:

(1)当t= ▲ 时,四边形PABQ是平行四边形;
(2)当t= ▲ 时,△PQF是等腰三角形.
【答案】
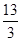 (1分);2或1或
(1分);2或1或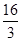 或
或 (对几个得几分,全对得5分)
(对几个得几分,全对得5分)
【解析】(1)设OP=2t,QB=t,PA=13-2t,要使四边形PABQ为平行四边形,则13-2t=t
∴ t=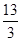
(2)∵OB∥DE∥PA,
∴ QB/AF=QE/EF=BD/DO=QD/DP= 12,
∴AF=2QB=2t,
∴PF=OA=13
①QP=FQ,作QG⊥x轴于G,则11-t-2t=2t+13-(11-t),
∴ t= ;
;
②PQ=FP,
∴ (11-3t)2+122=13,
∴ t=2或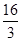 ;
;
③FQ=FP, [13+2t-(11-t)]2+122=13,
∴t=1;
综上,当 t= 或2或
或2或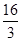 或1时,△PQF是等腰三角形
或1时,△PQF是等腰三角形

练习册系列答案
相关题目
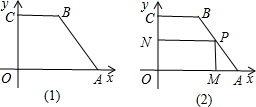 如图(1),在直角梯形OABC中,BC∥OA,∠OCB=90°,OA=6,AB=5,cos∠OAB=
如图(1),在直角梯形OABC中,BC∥OA,∠OCB=90°,OA=6,AB=5,cos∠OAB=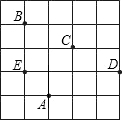
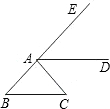

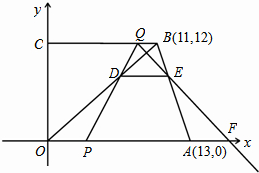 (2013•高淳县二模)如图,在直角梯形OABC中,OA∥BC,A、B两点的坐标分别为A(13,0),B(11,12).动点P、Q分别从O、B两点同时出发,点P以每秒3个单位的速度沿射线OA运动,点Q以每秒1个单位的速度沿线段BC运动,当点Q运动到C点时,P、Q同时停止运动,动点P、Q运动时间为t秒.设线段PQ和OB相交于点D,过点D作DE∥OA交AB于点E,射线QE交x轴于点F.
(2013•高淳县二模)如图,在直角梯形OABC中,OA∥BC,A、B两点的坐标分别为A(13,0),B(11,12).动点P、Q分别从O、B两点同时出发,点P以每秒3个单位的速度沿射线OA运动,点Q以每秒1个单位的速度沿线段BC运动,当点Q运动到C点时,P、Q同时停止运动,动点P、Q运动时间为t秒.设线段PQ和OB相交于点D,过点D作DE∥OA交AB于点E,射线QE交x轴于点F. 如图,在直角梯形OABC中,AB∥OC,BC⊥x轴于点C,A(1,2),C(3,0).动点P从O点出发,沿x轴正方向以每秒1个单位长度的速度移动.过P点作PQ⊥直线OA,垂足为Q.设P点移动的时间为t秒(0<t≤7),△OPQ与直角梯形OABC重叠部分的面积为S.
如图,在直角梯形OABC中,AB∥OC,BC⊥x轴于点C,A(1,2),C(3,0).动点P从O点出发,沿x轴正方向以每秒1个单位长度的速度移动.过P点作PQ⊥直线OA,垂足为Q.设P点移动的时间为t秒(0<t≤7),△OPQ与直角梯形OABC重叠部分的面积为S.