Question

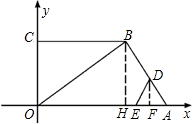
如图，在直角梯形OABC中，OA、OC边所在直线与x、y轴重合，BC∥OA，点B的坐标为（6.4，4.8），对角线OB⊥OA．在线段OA、AB上有动点E、D，点E以每秒2厘米的速度在线段OA上从点O向点A匀速运动，同时点D以每秒1厘米的速度在线段AB上从点A向点B匀速运动．当点E到达点A时，点D同时停止运动．设点E的运动时间为t（秒），
（1）求线段AB所在直线的解析式；
（2）设四边形OEDB的面积为y，求y关于t的函数关系式，并写出自变量的t的取值范围；
（3）在运动过程中，存不存在某个时刻，使得以A、E、D为顶点的三角形与△ABO相似，若存在求出这个时刻t，若不存在，说明理由．

Answer 1

分析：（1）根据相似三角形的判定得出△BOH∽△BOA，进而得出A点坐标，再由点B的坐标为（6.4，4.8），利用待定系数法求出解析式即可；
（2）过点D作DF⊥OA，垂足为F，DF∥BH，得出△ADF∽△ABH，得出DF=0.8t，进而得出S_△ADE的值以及y与t的关系式；
（3）分别根据①∠ADE=90°，当

AD

AB

=

AE

AO

时，△ADE∽△ABO，以及②∠AED=90°，当

AD

AO

=

AE

AB

时，△AED∽△ABO，得出答案即可．

解答：解：（1）过点B作BH⊥OA，垂足为点H，
∵∠COA=90°，BC∥OA，
∴∠BCO=90°，
∴四边形COHB是矩形，
∴BH=CO，BC=OH，
∵B（6.4，4.8），
∴OH=6.4，BH=4.8，
∴OB=

6.42+4.82

=8；
∵OB⊥BA，
∴∠OBA=90°，
∴∠OBA=∠OHB=90°，
∵∠BOH=∠AOB，
∴△BOH∽△BOA，
∴

BO

AO

=

HO

BO

，
∴OB²=AO•OH
∴8²=OA•6.4，
OA=10，
∴AB=

102-82

=6，
∴A（10，0），
设直线AB的解析式为：y=kx+b，

10k+b=0 6.4k+b=4.8

，
解得：

k=- 4 3 b= 40 3

，
∴y=-

4

3

x+

40

3

；

（2）过点D作DF⊥OA，垂足为F．
∴DF∥BH，
∴△ADF∽△ABH，
∴

DF

BH

=

AD

AB

，

DF

4.8

=

t

6

，
DF=0.8t，
∵OE=2t，AE=10-2t，
S_△ADE=

1

2

AE•DF=

1

2

（10-2t）×0.8t=4t-

4

5

t²，
∴y=24-4t+

4

5

t²（0＜t≤5），

（3）分两种情况：
①∠ADE=90°，
∵∠BAO=∠DAE，
当

AD

AB

=

AE

AO

时，
△ADE∽△ABO，

t

6

=

10-2t

10

，
解得：t=

30

11

，
②∠AED=90°，
∵∠OAB=∠DAE，
当

AD

AO

=

AE

AB

时，
△AED∽△ABO，
∴

t

10

=

10-2t

6

，
解得：t=

50

13

，
∴当t=

30

11

或t=

50

13

秒时，以A、E、D为顶点的三角形与△ABO相似．

点评：此题主要考查了相似三角形的综合应用，将动点静止在某一时刻，转化为相关三角形的知识求解是解题关键．