题目内容
【题目】综合题
(1)操作发现:
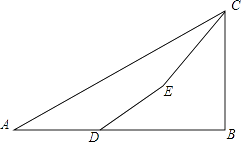
如图①,在正方形ABCD中,过A点有直线AP,点B关于AP的对称点为E,连接DE交AP于点F,当∠BAP=20°时,则∠AFD=°;当∠BAP=α°(0<α<45°)时,则∠AFD=;猜想线段DF,EF,AF之间的数量关系:DF﹣EF=AF(填系数);
(2)数学思考:
如图②,若将“正方形ABCD中”改成“菱形ABCD中,∠BAD=120°”,其他条件不变,则∠AFD=;线段DF,EF,AF之间的数量关系是否发生改变,若发生改变,请写出数量关系并说明理由;
(3)类比探究:
如图③,若将“正方形ABCD中”改成“菱形ABCD中,∠BAD=α°”,其他条件不变,则∠AFD=°;请直接写出线段DF,EF,AF之间的数量关系: .
【答案】
(1)45,![]() ,45
,45
(2)30
(3)解:(90﹣ ![]() ),DF﹣EF=2sin
),DF﹣EF=2sin ![]() αAF
αAF
【解析】【解析】解:(1)如图①中,连接BF、作AH⊥AF交DE于H.
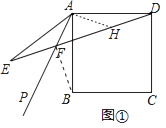
当∠PAB=20°时,
∵∠PAB=∠PAE=20°,∠BAD=90°,
∴∠EAD=130°,
∵AB=AE=AD,
∴∠E= ![]() (180°﹣130°)=25°,
(180°﹣130°)=25°,
∴∠AFD=∠E+∠PAE=45°,
当∠PAB=α时,∠E= ![]() [180°﹣(90°+2α)]=45°﹣α,
[180°﹣(90°+2α)]=45°﹣α,
∴∠AFD=∠E+∠PAE=45°﹣α+α=45°,
∵∠AFH=45°,∠FAH=90°,
∴AF=AH,
∵∠FAH=∠BAD=90°,
∴∠FAB=∠HAD,∵AB=AD,
∴△FAB≌△HAD,
∴BF=DH,
∵EF=BF,
∴DH=EF,
∴DF﹣EF=FH= ![]() AF,
AF,
所以答案是45,45, ![]() .
.
⑵如图②中,连接BF、作∠FAH=120°交DE于H,AM⊥DE于M.
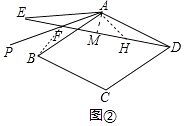
设∠PAB=α,
则∠E= ![]() [180°﹣(120°+2α)=30°﹣α,
[180°﹣(120°+2α)=30°﹣α,
∴∠AFD=∠E+∠PAE=30°,
∵∠EAH=∠BAD=120°,
∴∠FAB=∠HAD,
∵∠AFH=∠AHF=30°,
∴AF=AH,∵AB=AD,
∴△FAB≌△HAD,
∴BF=DH=EF,
∴DF﹣AF=DF﹣DH=FH,
∴AM⊥FH,AF=AH,
∴FM=MH=AFcos30°,
∴FH= ![]() AF,
AF,
∴DF﹣EF= ![]() AF,
AF,
所以答案是30,改变,DF﹣EF= ![]() AF
AF
⑶如图③中,当∠BAD=α时,设∠PAB=∠PAE=x,连接BF、作∠FAH=α交DE于H,AM⊥DE于M.
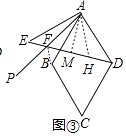
则∠E= ![]() [180°﹣(α+2x)=90°﹣
[180°﹣(α+2x)=90°﹣ ![]() α﹣x,
α﹣x,
∴∠AFD=∠E+∠PAE=90°﹣ ![]() α,
α,
∵∠EAH=∠BAD=α,
∴∠FAB=∠HAD,
∵∠AFH=∠AHF=90°﹣ ![]() α,
α,
∴AF=AH,∵AB=AD,
∴△FAB≌△HAD,
∴BF=DH=EF,
∴DF﹣AF=DF﹣DH=FH,
∴AM⊥FH,AF=AH,
∴FM=MH=AFsin ![]() α,
α,
∴FH=2sin ![]() αAF,
αAF,
∴DF﹣EF=2sin ![]() αAF.
αAF.
所以答案是(90﹣ img src="http://thumb.zyjl.cn/questionBank/Upload/2018/02/24/01/d9b95732/SYS201802240151098887506597_DA/SYS201802240151098887506597_DA.002.png" width="9" height="32" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" /> ),DF﹣EF=2sin ![]() αAF.
αAF.
(1)如图①中,连接BF、作AH⊥AF交DE于H.根据∠AFD=∠E+∠PAE=45°求出∠E即可解决问题;只需要证明△FAB≌△HAD,就可得出结论DF﹣EF=FH=![]() AF解决问题;(2)如图②中,结论:30°,改变,DF﹣EF=
AF解决问题;(2)如图②中,结论:30°,改变,DF﹣EF= ![]() AF,连接BF、作∠FAH=120°交DE于H,AM⊥DE于M.只需要证明△FAB≌△HAD,FH=
AF,连接BF、作∠FAH=120°交DE于H,AM⊥DE于M.只需要证明△FAB≌△HAD,FH= ![]() AF即可;(3)结论(90﹣
AF即可;(3)结论(90﹣ ![]() ),DF﹣EF=2sin
),DF﹣EF=2sin ![]() αAF.如图③中,当∠BAD=α时,设∠PAB=∠PAE=x,连接BF、作∠FAH=α交DE于H,AM⊥DE于M.证明方法类似。
αAF.如图③中,当∠BAD=α时,设∠PAB=∠PAE=x,连接BF、作∠FAH=α交DE于H,AM⊥DE于M.证明方法类似。
【考点精析】认真审题,首先需要了解菱形的性质(菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半),还要掌握正方形的性质(正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形)的相关知识才是答题的关键.

 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案【题目】中华文明,源远流长;中华汉字,寓意深广,为了传承优秀传统文化,某校团委组织了一次全校3000名学生参加的“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分.为了更好地了解本次大赛的成绩分布情况,随机抽取了其中200名学生的成绩(成绩x取整数,总分100分)作为样本进行整理,得到下列不完整的统计图表:
成绩x/分 | 频数 | 频率 |
50≤x<60 | 10 | 0.05 |
60≤x<70 | 30 | 0.15 |
70≤x<80 | 40 | n |
80≤x<90 | m | 0.35 |
90≤x≤100 | 50 | 0.25 |
请根据所给信息,解答下列问题:
(1)m= ,n= ;
(2)请补全频数分布直方图;
(3)若成绩在90分以上(包括90分)的为“优”等,则该校参加这次比赛的3000名学生中成绩“优”等约有多少人?