题目内容
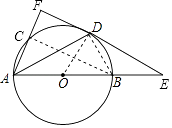
【题目】如图,AB是⊙O的直径,且AB=6,C是⊙O上一点,D是 ![]() 的中点,过点D作⊙O的切线,与AB,AC的延长线分别交于点E,F,连接AD.
的中点,过点D作⊙O的切线,与AB,AC的延长线分别交于点E,F,连接AD.
(1)求证:AF⊥EF;
(2)填空:
①当BE=时,点C是AF的中点;
②当BE=时,四边形OBDC是菱形.
【答案】
(1)解:连接OD,BD,BC,
∵ED为⊙O的切线,
∴OD⊥EF,
∵D是 ![]() 的中点,
的中点,
∴OD⊥BC,
∴EF∥BC,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠AFE=90°,
∴AF⊥EF;
(2)6,3
【解析】(2)①当BE=6时,
解:由(1)知,BC∥EF,当AB=BE时,AC=CF,
∴当BE=6时,点C是AF的中点,
所以答案是:6;
②当BE=3时,
解:∵AB是⊙O的直径,AB=6,
∴OB=OD=OC=BE=3,
∵ED为⊙O的切线,
∴OD⊥EF,
∴BD=OB=BE,
∵D是 ![]() 的中点,
的中点,
∴CD=BD,
∴CD=BD=BO=OD,
四边形OBDC是菱形.
所以答案是:3.
【考点精析】认真审题,首先需要了解菱形的判定方法(任意一个四边形,四边相等成菱形;四边形的对角线,垂直互分是菱形.已知平行四边形,邻边相等叫菱形;两对角线若垂直,顺理成章为菱形),还要掌握垂径定理的推论(推论1:A、平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧B、弦的垂直平分线经过圆心,并且平分弦所对的两条弧C、平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧;推论2 :圆的两条平行弦所夹的弧相等)的相关知识才是答题的关键.

 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案【题目】为了解某校九年级学生的身高情况,随机抽取部分学生的身高进行调查,利用所得数据绘成如图统计图表:
频数分布表
身高分组 | 频数 | 百分比 |
x<155 | 5 | 10% |
155≤x<160 | a | 20% |
160≤x<165 | 15 | 30% |
165≤x<170 | 14 | b |
x≥170 | 6 | 12% |
总计 | 100% |
(1)填空:a=____,b=____;
(2)补全频数分布直方图;
(3)该校九年级共有600名学生,估计身高不低于165cm的学生大约有多少人?